I have, at last, readed the following article of Leonard Suskind on the antropic landscape:
http://arXiv.org/hep-th/0302219 v1
Before briefly discusing it I will mention that I have also beeing reading the chpater on cosmology of dinés book "supersymmetry and string theory" and some stuff on blogs and forums about cosmology. I must say first that a few years ago (maybe a decade) the view of cosmology among theoretical physics (or at least the ones I speaked too) was diferent that what actually is. The viewpoint was that there were physic firmely based on carefull and exaustives experiments made in earth, which were the core of physics and that as an interesting toy you could try to aply that laws to the universe as a whole and to see how well it fitted. The consensous was that the important aspect was that the universe could be coarse grained described by a, relatively, very simple models. If there was some particular deviation it was a good thing to try to improve the models to fit it, but it was not a preferent problem.
A good reason for not taking too seriously cosmology is that the universe as a whole is a very bad experiment. There are too many possible variables (some of them probably ignored) playing in complicated manners. In an earth based experiment you can modify the settings so that only a few parameters are relevant for the quantity you try to messure, but you can´t do something similar with the whole universe.
But from a time to now the viewpoint has drastically changed. The string theory comunity have the viewpoint that it is very unlikely to see quantum gravity effects in colliders (an exception could arise if brane universe scenaries are correct) and, in general, another stringy effects are also hard to see. On the countrary the early universe, with it´s high energy, would be the place to search for this efffects. I must´say that I have become surprised when I have seen some of the effort made in this line of research. To say one I never even had thoguht that someone could have cared about the possibility that the decayof a gravitino, the supertpartner of the graviton, could be dominant at the same time that baryogénesis and that it could rsult in breaking of light elements. Or that a similar situtation could exist fo rmoduli fields of supersymmetry or string theory. There are workarounds for this posibilities, of course, but, what the hell? Who cares?. I mean, the interest is to find signs of supersymmetry now, not in some scenaries that could have existed, but that are excluded by observation.
But, ok, If some people wants to work in that things is fine for me. Even better is that people could be using string theory to calculate potentials for inflaton fields when they previously introduced that potentials by hand to try to fit observaations. The LQG comunity are using extensively the canonical (hamiltonian) aproach to do a lot of toy models. Irrespectively of how good or bad you thnk about LQG their effort is coherent in their internal logic.
In general I don´t dislike when people are triying to use fundamental physics (or should be physics,i.e. non still proved theories like strings and LQG) to see how they can help to fit cosmological observations. My problem is when the flow is in the reverse direction, when people try to modify physics (or should be physic) froms cosmological observations. A previous aclaration is necessary. If some theory predicts an aboundancy of phenomena such as monopolesor cosmic strings and hthat boundance is not observed one, certainlly, need tobe cauptios with that particular model. That is, one could be aware that the model can´t be the final answer to unification physics (althought still could be that some factor is the cause of the nonobserved aboundances and the model still be valid). But one would not rule out a model, with physical consecuences of it observed in earth, because of cosmological situations. Nor one would leave the traditional way to do physic because or cosmological observations.
Well, as everybody who knows the actual state of string theory knows this is not the case. The observation of an small positive cosmological constant has hanged the way to do physic (or at least string theory). The problem with that cosmologial constant is that string theory, as well as any quantum field theory for what matters, has a problem to explain it. If one calculates for an ordinary QFT the vacuun energy one finds that it is aan few orders of magnitude higher than the observed cosmological constant. If one has a supersymmetric theory, with unbroken supersymmetry, bosonic and fermionic modes canell out and one can get a 0 cosmological constant. The "little" problem with it is that suposedly supersymmetry is broken.
Well, the problem has existed from a long time, would it be with 0 or with a tiny cosmological constant. And people has lived with the problem and has been happy doing physics. But now it results that string theorists had a good confidence that afther all string theory could fit well with a 0 cosmological constant. And when the have found that it could be non zero (the experimental status of this is good, with at least 3 partially unrelated phenomenae indicating it, but still there are possibilities that afther all it is 0) the have become nervous and have modified the way to thnk about string theory, and it´s vacuums, to accommodate the reslt. In fact they have beein inspired by a model made by Weinberg a few decades ago. A model who was nothing but a curiosity who none cared too much because the had more interesting things to study.
But now you must leave with the idea that the universe must be in a sperposition fo supersymmetric vacuums, with 0 CC, and nonsupersymmetric ones, with a big CC, so the promedium is the observed one. Even you must face the possibility that this low value is hold only in a, relatively small, part of the universe separated by horizonts from anothers. And the criteria (while someone finds something better) to make physics in this superposition of vacua is to use anthropic principles.
Well, nowadays even renuent people such like Lubos Motl, seems to accept this status. My viewpoint is that there are a lot of things to do in string theory (or out of it) which is mainly unafectd by this change of paradigma. So, beyond being to the expectative that somone finds a better solution to the CC problem, I wouldn´t care too much about that landscape and would worry about other things, at least if that is possible (and I guess it will be).
Wednesday, December 05, 2007
Saturday, November 24, 2007
The phenomenology, the abstract theory and the weird speculation
I am almost sure that if some high end professional of string theory hs readed the previous entry vill have renewed his very bad thoughts about the physics blogosphere. If, instead, he would have readed the post about Horava-Witten theory and brane univereses I guess taht he instead will have felt more confortable. This is because the post of topology vs group theory was speculative, probably too speculative (althought not necesarily a nonsense I hope), while the one in brane universes was very conventional and not controversial at all. In fact I could have made something similar and I could have limited myself to enumarate some of the many, many well stablished aplications of topology to physics, explaingn briefly the details and by signaling it´s numerical and conceptual superiority over the group theory aplications and I would have a "safe" post. In fact I´ll probably do some of this in posterior entries, but that wouldn´t show the viewpoint I wanted to transmite.
Afther this I am going to explain the reason of the topic. In physics, even in theoretical physics, there are many levels. One one side there are the "old fashioned" particle physicis. You can find some of them, teachers with academic positions in good universities, which hate even the yang mills theory as explained, for example, in the Cheng and Li book of particle physics, (or in any conventional QFT text book for what matters). They prefer the very heurisitc exposition of the subject presented in books such like the one of Halzen and Martin "quarks and leptons". This people usually like "solid physics" from colliders. In an intermediate, most reasonable, state are phenomenological people who accept and like QFT. This people can be working on hadron physiscs or even dealing with some posible phenomenology related to supersymmetrtry, mainly the MSSM (minimally supersimmetric standard model) and supersymmetric unification. Some even go beyond and are interested in string theory or (possible) alternatives to quantum gravity.
To read books for this people is a very good way to learn actually stablished physics and possible near future physics. I know two great books of this characteristics. The excelent one of Martin, squires and Collins "particle physics and cosmology", and the very recent one of Michel Dine "Supersymmetry and String theory". In some sense the last one is an (unintended) update of the previous. To be honest I find more understable and better writen the one Martin et all that the book of Dine. But still is a good book. The introduction to supersimmetry is very diferent, and the book of Amrtin et all includes also supergravity. On the other since the Dine´s books goes a lot deeper into string theory, withouth beeing a rigurous book on pure string theory (of course because that was not i´s purpose). I guess that everyone should read some book of this characteristics from time to time to keep contact with the details of phenomenology.
But detailled phenomenology is not everything in theoretical physics. You need to give good foundation to the enviroment in which the pheonomnological calculations are done. This requires at least to understand the proper foundations of quantum field theory and supersymmetry. A good modern exposition wuld be the three volumes book of Weinberg, but honestly, I see that book more like a reference book that anything else. A poit that string theorist signal is that one should be sure to study modern renormalization theory (It is not the same as the renormalization theory in classic QFT books such like the Itzikson-Zuber). I am doing this just now. I did a bad coice of review article that has delayed me for a time, but I guess that I am beguining to gain proper understanding of it. Beyond QFT there is supersymmetry. The books I mentioned previously are "all purpposed books" but there are textbooks specialized in supergravity. I have ocassionaly readed one (but unfortunately it is not in a very asscessible place now so I cant give you the exact reference). They concentrate in more theoretical aspects of supersymmetry and while string theory is a much more promising area of study they still have their point.
And of course we have string theory, and all the possible alternatives. That are pure theory. In fact still instring theory there are more "phenomenological" aspects, for example to find realistics compactifications or to solve the cosmological prblem, and more "theoretical aspects". Of this last I could signal to try to understand better what M-theory is, the superstring field theories, and the Maldacena conjecture, to say ones. Other topics, for example black hole theory, are somewhat in the middle.
And now the last topic, the "weird speculation". This is a broad subject. It can go from simple tings, like to get a proper understanding of the theories to more risked things. I´ll give a few examples of the first point. A very basic one is from nonrelativistic quantum mechanics, collision theory. When I was teached it I understood everything perfectly untill we arrived to resonances. Them the teacher explained you that the imaginary poles of the S-Matrix where resonances. Fine, it was a relatively easy thing to find that poles and to work with them. Inmediately later he toldd you that heuristically you would interprete that resonances as "metastable states". But he didn´t explain why. The book that he followed, and a fe other I readed, didn´t say more. Of course for me this was totally unsatisfactory. I could pass the exam withouth mayor problem even doing an exercise about resonances. But from my viewpoint I didn´t understand resonances at all. I asked the quesetion from time to time, but it was not untill that I casually readed the Landau chapter in the subject. There they explained why this math prescription came. You neded to think in outgoing waves with imaginary exponent and how this was related to the metastability (read the book for the details if you don´t know them, It is a total "you must").
In QFT I havent´t found (or at least I don´t remmeber them now) similar situations. But in strign theory I have found many. To beguin the very basic idea of string theory, such as I explained in the first entries of this blog. To read all the modern boooks on the subject didn´t convince me a bit that the idea of an string, such as presented, is a convincing one. Like string theoriest don´t care too much about it I try to do "weird speculation" about the subject. My initial idea of knotted strings is easy to state in a formal way. Afther reading the chapter 13 (if Idon´t remmember bad) of the Green -Schwartz-Witten bookd I have gained the knowledge that open strings can join their endpoints and to form a closed string. Well, aparently two open strings could get closed interlinking one to another. You would describe the collective state by a hilbert product state of the separate strings. If this configuration would be stable you would have states that would look like mixed states of conventinal particles. To elucidate aobut if this stability could exist I must go to another theory. Rañeda and Trueba made a topological formulation of electromagnetism. This consisted of expresing the vacuum Maxwell equations in terms of different fields. This allowed them to clasify the solutions with bounded energy (i.e. vanishing in the infinity) into topological sectors with different of a topological quantity which could be identified with the heilicity of the electromagnetic field. The configurations with non trivial topology (identificalbe, among another possible ways, as a kind of knoting) presented extra stability, and it was conjetures that they could be related to the atsosferic pehnomenon know as "ray balls" (the actual article is published in nature, so be totally sure it is not "crackpot phuysic"). The idea could possibly be extended to Yang Mills theories. ANd here is where I think that it could be connected somehow to this "knotted strings" . If the string which get knotted are in a vibrational state corresponding to yang mill fields it could be that they could be somehow resemble some knotted configuration of Yang Mill fields and become stable. Of course this is very wild speculation, and withouth confronting more detaills and consistency checks is not something to be considered seriously.
The key point of knotted strigs is that if one takes serioulsy the idea of string theory they I.M.H.O. would be considered (soon I´ll explain another possible argument). But I still am dissapointed with the idea of strings. I am triying to search for a natural way inwhich strigns make sense (and don´t disgregate intoit´s constituent points). I knowt thaat one should addopt the coherence of the string as a postulate. But I still try to go beyond that. From the accepted string theoretical viewpoit there are a few possible aproachs to it that I try to consider. S-duality relate the strong coupling limit of an string theory to the weak coupling limt of another. Under this duality fundamental strings of a theory canbe identified with D1-branes of the other. But D1-Branes suposedly can be charasterized as some kind of topological deffects. Topological deffects are stable things, so that could justify a posteriory the stability of fundamental strings. The problem is that to arrive to the D-brane idea one must beguin with perturbative strings. There is the viewpoint of "D-brane democracy". This means that dpednidn on energy,or maybe better said, inthe history of the universsee, of thepossible equivalent ways to describe string theoyr (all the five strig theorys, M-theory and F-theory) the universe is in an state in chich "fundamental" strings are agood description of observable physic, but still the reason of their stability must be explained in the D1-Brane ansatz.
A more drastic departure to try to assign a "naturality" to the idea of string (here is where the profesional string theorisst will definitively lose it´s patience if he has resisted untill this pint) could come from the following scenary. In some aspects thje idea of string separates the universe intotow scales. The scale greater than the string and the scale smaller (In fact d-branes canprobe distances smaller than the size of an string, but let´s accept the premise for a while). Well, let´s try to get the same idea in a diferent viewpoint. We must have an "inner theory" for distances smaller than the planck scale that in the limits reproduce ordinary quantum field theory. Under the planck size the usuall notions of QFT and relativity (in particular the Lorentz invariance) would dissapear, or more properly said, they could not experimentally stablished. That would mean that if we try to be sure that if a particular state is an electron, a photon or whatever in distances shorter than the panck one we cant so we must deal with states that are a superpostion of all the possibilities. String are good for it. Of course this is not more than cheap philosophy in this state. Another way totry to sse this I gues that it can be related to M-theory. While reading about horava-witten theory I have got more involved withthe bizarre aspects of M-theory. FOr example there are arguments that it´s proper description cant be given in termos of a lagrangian. This means that it doesnt go under the prescription of a variational principle. There are not classical configurations that minimize and action and quantum corrections. But this means that we are in a democracy where every trajectory is equally good, and there is not quantum physic. On the other hand M-Theory is the strong coupling constant of string theory. I am not totally sure but i think than that means that it studies the behaviour of the shortes vibrational modes of the string. This modes somehow would explore a region where evrything is beyond the planck scale. AS the planck constant has magnitudes of action whe are exploringn zones wher the notion of action does´nt apply. This could explain why there is no lagrangian (i.e. action based) description of M-theory. Once agian, this is weird, and weak, and cheap speculation. Dont confuse it with anything accepted by the mainstream os string theorists.
Another thing in string theory which I want to understand properly is why D-branes are suposed to be infinitely extended. If a D1-brane is the dual oof a fundamental string, a very shor object, why the hel it must be infinitellly extended .Somone pointed me that infact a priory it wouldn´t be necesary, but that stabiilty reasons force one to have infinitely extendend D-branes. Well, I don´t know where that calculations are done, may be inthe K-theory program, in the analisys ob non BPS branes, it could be related to th tachyonic condnesation, or maybe it is explained in some arkane text about the M-branes. At least now I have the certainty that it is not a trivial thing and that the a priory idea that D-branes would be of a finite size was a reasonable question. B.T.W., I had said that tere were another possible way to explain ths stability of "knotted stirngs" if that configuartios would form. Of course that would be seen to come from a D1-Brane perspective. If infinite sized branes cross among them it looks like that would be very stable topologicaly.
This was weird speculation within string theory. Now I am going to say an example of speculation outside it. Pitkannen proposes in it´s topological geometrodynamic that oneshould worry about the possibiilty that because of some reasonone would care about p-adic metrics. In a p-adic metric ponts very far away inthe conventional metric are very nearby. I think that he try to present an scenary where the nature of the real world is p-adic (at least in some cases). That would explain, inhis viewpoint the colapse of the wavefunction. He subscribes a viewpoint where concsciece is related to that, and it implies that humans brians have the capability to ifluence long distances. Well, maybe he would like becuase of this some weird paper (commented inLubos blog) that hte observation of the cosmological constant has modifeid the stae of the universe, or maybe not, you can ask him in his own blog. What I wondered yesterday was nothing of this. I had said that if one tries togive a ynnamical topology change, explianing the formation of a wormhole, it appear natural to expect that it connects nearby distnces. Infact quantum fluctuation (basically here the usual Heisenberg uncertainty betwen postion and momenta)could justify an small posibity that it would connect far points. But, if in some range the nature is actually best described by p-adic (or adelic) metrics (afther all there are people worriying about p-adic strings) then it would be natural that wormholes afther ll would connect points that in the ordinary metric are far away .
Well, I hope that if I am very clear staitng when I speak about accepted physics and when i am divagating (and triying to pose a quote to the degree of divagation) the reader can actually have a realistic perspective of physics, and maybe somes even fun (interesting would be a too exigent word) fan the weird speculations. Anyway, I´ll try to post mainly about divulgation of conventionally accepted physics.
Afther this I am going to explain the reason of the topic. In physics, even in theoretical physics, there are many levels. One one side there are the "old fashioned" particle physicis. You can find some of them, teachers with academic positions in good universities, which hate even the yang mills theory as explained, for example, in the Cheng and Li book of particle physics, (or in any conventional QFT text book for what matters). They prefer the very heurisitc exposition of the subject presented in books such like the one of Halzen and Martin "quarks and leptons". This people usually like "solid physics" from colliders. In an intermediate, most reasonable, state are phenomenological people who accept and like QFT. This people can be working on hadron physiscs or even dealing with some posible phenomenology related to supersymmetrtry, mainly the MSSM (minimally supersimmetric standard model) and supersymmetric unification. Some even go beyond and are interested in string theory or (possible) alternatives to quantum gravity.
To read books for this people is a very good way to learn actually stablished physics and possible near future physics. I know two great books of this characteristics. The excelent one of Martin, squires and Collins "particle physics and cosmology", and the very recent one of Michel Dine "Supersymmetry and String theory". In some sense the last one is an (unintended) update of the previous. To be honest I find more understable and better writen the one Martin et all that the book of Dine. But still is a good book. The introduction to supersimmetry is very diferent, and the book of Amrtin et all includes also supergravity. On the other since the Dine´s books goes a lot deeper into string theory, withouth beeing a rigurous book on pure string theory (of course because that was not i´s purpose). I guess that everyone should read some book of this characteristics from time to time to keep contact with the details of phenomenology.
But detailled phenomenology is not everything in theoretical physics. You need to give good foundation to the enviroment in which the pheonomnological calculations are done. This requires at least to understand the proper foundations of quantum field theory and supersymmetry. A good modern exposition wuld be the three volumes book of Weinberg, but honestly, I see that book more like a reference book that anything else. A poit that string theorist signal is that one should be sure to study modern renormalization theory (It is not the same as the renormalization theory in classic QFT books such like the Itzikson-Zuber). I am doing this just now. I did a bad coice of review article that has delayed me for a time, but I guess that I am beguining to gain proper understanding of it. Beyond QFT there is supersymmetry. The books I mentioned previously are "all purpposed books" but there are textbooks specialized in supergravity. I have ocassionaly readed one (but unfortunately it is not in a very asscessible place now so I cant give you the exact reference). They concentrate in more theoretical aspects of supersymmetry and while string theory is a much more promising area of study they still have their point.
And of course we have string theory, and all the possible alternatives. That are pure theory. In fact still instring theory there are more "phenomenological" aspects, for example to find realistics compactifications or to solve the cosmological prblem, and more "theoretical aspects". Of this last I could signal to try to understand better what M-theory is, the superstring field theories, and the Maldacena conjecture, to say ones. Other topics, for example black hole theory, are somewhat in the middle.
And now the last topic, the "weird speculation". This is a broad subject. It can go from simple tings, like to get a proper understanding of the theories to more risked things. I´ll give a few examples of the first point. A very basic one is from nonrelativistic quantum mechanics, collision theory. When I was teached it I understood everything perfectly untill we arrived to resonances. Them the teacher explained you that the imaginary poles of the S-Matrix where resonances. Fine, it was a relatively easy thing to find that poles and to work with them. Inmediately later he toldd you that heuristically you would interprete that resonances as "metastable states". But he didn´t explain why. The book that he followed, and a fe other I readed, didn´t say more. Of course for me this was totally unsatisfactory. I could pass the exam withouth mayor problem even doing an exercise about resonances. But from my viewpoint I didn´t understand resonances at all. I asked the quesetion from time to time, but it was not untill that I casually readed the Landau chapter in the subject. There they explained why this math prescription came. You neded to think in outgoing waves with imaginary exponent and how this was related to the metastability (read the book for the details if you don´t know them, It is a total "you must").
In QFT I havent´t found (or at least I don´t remmeber them now) similar situations. But in strign theory I have found many. To beguin the very basic idea of string theory, such as I explained in the first entries of this blog. To read all the modern boooks on the subject didn´t convince me a bit that the idea of an string, such as presented, is a convincing one. Like string theoriest don´t care too much about it I try to do "weird speculation" about the subject. My initial idea of knotted strings is easy to state in a formal way. Afther reading the chapter 13 (if Idon´t remmember bad) of the Green -Schwartz-Witten bookd I have gained the knowledge that open strings can join their endpoints and to form a closed string. Well, aparently two open strings could get closed interlinking one to another. You would describe the collective state by a hilbert product state of the separate strings. If this configuration would be stable you would have states that would look like mixed states of conventinal particles. To elucidate aobut if this stability could exist I must go to another theory. Rañeda and Trueba made a topological formulation of electromagnetism. This consisted of expresing the vacuum Maxwell equations in terms of different fields. This allowed them to clasify the solutions with bounded energy (i.e. vanishing in the infinity) into topological sectors with different of a topological quantity which could be identified with the heilicity of the electromagnetic field. The configurations with non trivial topology (identificalbe, among another possible ways, as a kind of knoting) presented extra stability, and it was conjetures that they could be related to the atsosferic pehnomenon know as "ray balls" (the actual article is published in nature, so be totally sure it is not "crackpot phuysic"). The idea could possibly be extended to Yang Mills theories. ANd here is where I think that it could be connected somehow to this "knotted strings" . If the string which get knotted are in a vibrational state corresponding to yang mill fields it could be that they could be somehow resemble some knotted configuration of Yang Mill fields and become stable. Of course this is very wild speculation, and withouth confronting more detaills and consistency checks is not something to be considered seriously.
The key point of knotted strigs is that if one takes serioulsy the idea of string theory they I.M.H.O. would be considered (soon I´ll explain another possible argument). But I still am dissapointed with the idea of strings. I am triying to search for a natural way inwhich strigns make sense (and don´t disgregate intoit´s constituent points). I knowt thaat one should addopt the coherence of the string as a postulate. But I still try to go beyond that. From the accepted string theoretical viewpoit there are a few possible aproachs to it that I try to consider. S-duality relate the strong coupling limit of an string theory to the weak coupling limt of another. Under this duality fundamental strings of a theory canbe identified with D1-branes of the other. But D1-Branes suposedly can be charasterized as some kind of topological deffects. Topological deffects are stable things, so that could justify a posteriory the stability of fundamental strings. The problem is that to arrive to the D-brane idea one must beguin with perturbative strings. There is the viewpoint of "D-brane democracy". This means that dpednidn on energy,or maybe better said, inthe history of the universsee, of thepossible equivalent ways to describe string theoyr (all the five strig theorys, M-theory and F-theory) the universe is in an state in chich "fundamental" strings are agood description of observable physic, but still the reason of their stability must be explained in the D1-Brane ansatz.
A more drastic departure to try to assign a "naturality" to the idea of string (here is where the profesional string theorisst will definitively lose it´s patience if he has resisted untill this pint) could come from the following scenary. In some aspects thje idea of string separates the universe intotow scales. The scale greater than the string and the scale smaller (In fact d-branes canprobe distances smaller than the size of an string, but let´s accept the premise for a while). Well, let´s try to get the same idea in a diferent viewpoint. We must have an "inner theory" for distances smaller than the planck scale that in the limits reproduce ordinary quantum field theory. Under the planck size the usuall notions of QFT and relativity (in particular the Lorentz invariance) would dissapear, or more properly said, they could not experimentally stablished. That would mean that if we try to be sure that if a particular state is an electron, a photon or whatever in distances shorter than the panck one we cant so we must deal with states that are a superpostion of all the possibilities. String are good for it. Of course this is not more than cheap philosophy in this state. Another way totry to sse this I gues that it can be related to M-theory. While reading about horava-witten theory I have got more involved withthe bizarre aspects of M-theory. FOr example there are arguments that it´s proper description cant be given in termos of a lagrangian. This means that it doesnt go under the prescription of a variational principle. There are not classical configurations that minimize and action and quantum corrections. But this means that we are in a democracy where every trajectory is equally good, and there is not quantum physic. On the other hand M-Theory is the strong coupling constant of string theory. I am not totally sure but i think than that means that it studies the behaviour of the shortes vibrational modes of the string. This modes somehow would explore a region where evrything is beyond the planck scale. AS the planck constant has magnitudes of action whe are exploringn zones wher the notion of action does´nt apply. This could explain why there is no lagrangian (i.e. action based) description of M-theory. Once agian, this is weird, and weak, and cheap speculation. Dont confuse it with anything accepted by the mainstream os string theorists.
Another thing in string theory which I want to understand properly is why D-branes are suposed to be infinitely extended. If a D1-brane is the dual oof a fundamental string, a very shor object, why the hel it must be infinitellly extended .Somone pointed me that infact a priory it wouldn´t be necesary, but that stabiilty reasons force one to have infinitely extendend D-branes. Well, I don´t know where that calculations are done, may be inthe K-theory program, in the analisys ob non BPS branes, it could be related to th tachyonic condnesation, or maybe it is explained in some arkane text about the M-branes. At least now I have the certainty that it is not a trivial thing and that the a priory idea that D-branes would be of a finite size was a reasonable question. B.T.W., I had said that tere were another possible way to explain ths stability of "knotted stirngs" if that configuartios would form. Of course that would be seen to come from a D1-Brane perspective. If infinite sized branes cross among them it looks like that would be very stable topologicaly.
This was weird speculation within string theory. Now I am going to say an example of speculation outside it. Pitkannen proposes in it´s topological geometrodynamic that oneshould worry about the possibiilty that because of some reasonone would care about p-adic metrics. In a p-adic metric ponts very far away inthe conventional metric are very nearby. I think that he try to present an scenary where the nature of the real world is p-adic (at least in some cases). That would explain, inhis viewpoint the colapse of the wavefunction. He subscribes a viewpoint where concsciece is related to that, and it implies that humans brians have the capability to ifluence long distances. Well, maybe he would like becuase of this some weird paper (commented inLubos blog) that hte observation of the cosmological constant has modifeid the stae of the universe, or maybe not, you can ask him in his own blog. What I wondered yesterday was nothing of this. I had said that if one tries togive a ynnamical topology change, explianing the formation of a wormhole, it appear natural to expect that it connects nearby distnces. Infact quantum fluctuation (basically here the usual Heisenberg uncertainty betwen postion and momenta)could justify an small posibity that it would connect far points. But,
Well, I hope that if I am very clear staitng when I speak about accepted physics and when i am divagating (and triying to pose a quote to the degree of divagation) the reader can actually have a realistic perspective of physics, and maybe somes even fun (interesting would be a too exigent word) fan the weird speculations. Anyway, I´ll try to post mainly about divulgation of conventionally accepted physics.
Topology vs group theory in physics
I have said in some ocations that I dont´t like too much group theory, and that I prefer to study topology. I am going to try to explain a litle bit about it.
One of them is pureley mathemathical, I prefer to study things like homology, cohomology, sheaves, spectral sequences, cobordism, morse theory, K-theory and mostly all the topology in the world than group theory. Group theory, and it´s representations, is more or less always the same, but there are a lot of diferent topological tools, all of them with their own peculiarities.
But maths is not a reason a physician could accept. Well, let´s go to physical motivations. One of the goodnes of topology is to try to decide what interestign things happen when one goes from the local tothe global. For example infixing a gauge for a gauge theory you have that any gauge fixing is local and that you can´t extend it to the whole of the phase space. One consecuence of it is the so called Gribov ambiguity. In fact there is a problem with this. Most topological theories are intended to study finite dimensional manifolds and the phase space of a gauge theory is not one of them, so the path is not straighforward from the topology books to their applications in this problems. For example, the BRST operator of gauge theories certainly has the same characteristics than the external derivative of diferential forms. You can form the de-Rham cohomology with the external derivative, to prove that it is equivalent to another cohomologies and use it as a calculational tool for finite manifolds. BRST is usefull, certainly, to select physical states, but I don´t see in the literature that it would be applied to analize the topology of the infinite dimensional phase space. Fortunately there are other things where topology, in its more straightforward form, is interesting, relativity.
One of the things that I find more interesting in general relativity is the role of topology change. The Einstein equations fix the metric of space-time, but don´t say anything specific about it´s topology. In most conventional problems the topology is somewhat assumed. For example in ths schwarschild solution you are studiying something which is topologicallly R3, or, if there is a black-hole you could doubt about the nature of the singularity and to deciede to excise it. Schwarschild space tie is static so it is not problematic. But wen you have a non static space-time things are more intringuing. At a given "time" you have an hypersurface (the technical key word is "slicing"). The natural questions is to wonder if time evolutions, given from the Einstein equations, could change the topology of that hypersurfaces from one time to another. That is a very mathemathically interesting problem in classical gravity and it is usually studied using cobordisms betwen the hypersurfaces. Cobordism intuitive idea is very easy to understand, you wonder when two given n-manifolds can be the border of another n+1-manifold. If you don´t whant to learn cobordism you simply can go to the results which states the criteria under a objects more best known to physicans, characterisitic classes. The results are that if you don´t impose aditional conditions you actually can have topology changes. But when you impose things such like causality and similars the things are more obscure and probably topology change is forbiden. I must say that even if you understand the detaills of the math involved it is somewhat surprising to try to thnk into the details. Afther all in one point you have a metric for a manifold, and later a metric fo ra diferent manifold. And somewhere in the midle you must have a metric which would be good for limit cases of that manifolds. Try to imagine a two dimensinal cae. For example the traditional idea of the formation of a whormhole. You beguin with a 2 sphere and you go nearing two points of it (think for simplicity of two opposite antipodal, points. In the limit beofore the change to the new topology you would have an sphere with the two antipodal points idetntifieds. Afther that you would have a torus.
Try to think about what´s going on just in the intermediate betwen the two cases. Inmediately before you have two tangent spaces which in the intermediate point must be identified. How to interpretate that physically? For that urpose I guess that topology is not the better tool and that the answer would rely in algebraic geometry. I am actually triying to learn algebraic geometry (beyond the one exposed in string theory books) so I can´t go further into this.
I have said "whormhole". Certainlly there is a lot of literature about them. But what I have readed doesn´t actually says too much about the topology change. For transversabble (minkowskian) wormholes you simple decide based in natural requirements a guess form for the metric. But it is all static, you describe the formed wormhole, not the process of it formation. Some tiem ago wormholes where considered funny curiosities usefull for science fiction tales. With the observation of the acclerated universe the thing has changed. The reason is that the existence of a cosmological constant, or of phanthom energy (another possible cause of the acelerating universe) give to wormholes a different position in physicis. The reason is that transversable womhholes require the existence of energy violating the weak energy condition. Usually it was thought that alghoutght it was possible to have small amounts of this matter (by means of quantum effects such like the cassimir effect) it was very unlikely to have too much of it. But the acclerated expansion of the universe make svery plausible that this matter exists. For example in the branworld universes you can have five dimensional matter which in five dimesnions doesn´t vilate that condtion but that it seems to do so in four. The main conclusion is that because of many possible realizations womrholes in a acceraated should exist, and that one must try to find a reason to explain why the don´t exist, or, better, to try to search for them. This could be possible, for example, triying to detect "macroscopic monopoles". The reason is that an usula magnetic field in the vecinity of a wormhole could appear as a magnetic monopole for some observers. Semengly there are concrete proposals for searching them, but I am not totally sure about how the are evolving.
By the way, note that I have said that wormholes are being heavilly studied in the braneworld scenaries. This is one of the reasons I have studied more in deep the Horava-Witten models. I didn´t feel confortable by only understandin the phenomemological approach. In the near future I´ll go back to the study of wormholes, both in conventinoal and in braneworld univeres, and not only to it´s static aspects but to try to understand the dynamics of the formation. If you are a fan of science fiction I can give you a reason why the could be interestings. In SF histories they are usually a tool for interestelar travel or a time machine. But if you think about it if you actually tri to construc a wormhole the most probable thing is that you would connect points that are (very) near one of them. Later you could try to separate the throats of the wormhole. They would be usefull as a fast interstellar travel device only afther you carry the throaths that distance by a conventional way (suposing that the inner distance bethwen the throats doesnt grow). But there is a possible, more realistic, and more usfull way to use a wormhole. You could put one throat near the sun surface and the other near the earth. The solar energy going inside the womrhole will not spread so you will send to the earth the same energy of the sun as the area of the throats. A crude estimation shows that a throat of a few metter of radius will send to the earth the energy that the human the whole race needs. Of course you need to use an intermediate energy vector to use that electromagnetic energy, but that are "minor detaills" xD.
Still one could think that wormholes, or topology change in general relativiey is a too restricitive field. I don´t think so. In string theory there is a great problem. Triying to seek a viable compactification (or going into the landscape if you like that things). But if one thinks a bit about it a compactification is ultimatelly a topology change in the underliying space. Almost all of the work is being done to try to seek for good compactifications. You use a lot of topology and algebraic geometry for that. That is because you study the topology of the resulting space, but you dont wonder how you arrive to that compactificated spaces. String theory goes beyond general relativity, but still it could be interesting to see what a general relativity (or something near to it) could say about that transitions. For example, what kind of matter would inforce that compactifications?
Until nw I have mainly mentioned topology, what about group theory? I am not going to alk too much about it, but, instead, I´ll try to relate it somewhat to compactifications. The easiest place where group theory can appear in quantum physics is in the theory of the angular momentum of a nonreltivistic particle. Rotations in space are described by the SO(3) group. Th universal covering group of SO(3) is SU(2). On the other hand when you have a quantum system with rotational invariane it can be said that, just like in the classical counterpart, the angular momentum is conserved. The classical angular momentum is L=rxp. If you go from the classical momentum p to the quantum operator p you have the definition for the quantum angular momentum. Youcan show that their component´s don´t conmute so you can only observe one of them simultaneously. On the other hand the squared angular momentum L2 conmutes with all the components so you can observe it. You can connec the physics with the group theory saying that L2 is a cassimir operator for a representation, and that you can relate L+- = Lx +- iLy which act as ladder operators, similar to the a+ a- of the harmonic oscilators, to elements of the group theory of SU(2).
This was an external symmetry. Latter, with the advance of particle physics and QFT appeared internal symmetries, and they were related to easy groups. SU(2), SU(3) and U(1). And the first unification attemp was SU(5). The same technicques used for the group theoyr tratement and a few others allowed to do a lot of calculatiions in particle physicis. Another point of group theory was the role played by the poincaré an dLorent group to the classifications of particles. One could relate the spin of a particle to a representations of the Lorentz group. Of course all of this is well known by a lot of the people that wouldmost likely wuld be interested in reading this blog, so which is my point against group theory.
I said that I wuld relate group theory and compactification. Afther all one of the points of stirn gtheory is to recover the ideas of Kaluza-klein. One can show (I did a post, in spanish, in this blog about it) that an five dimensional space compactified in a circle makes that the "external" gravitational of the five dimension becomes an U(1) "internal" simmetyr equivalent to electromagnetism. This is the ideal case. But nature is not allways ideal. In facto it usually isn´t. The hidrogen atom is almost perfectly shperically symmetric, but because of electron, electron-interaction other atoms are not. Still angular momentum is a very usefull quantity, but it doesntt any more is related to a perfect "reall" symmetry.
What about the circle of the compactification?. On could expect that it would be a perfect circle. Afther all symmetric configurations are commonly the right solutions for optimization problems. But if we think in the possible dynamic of the compactification one realize that that circle still i space-time, and because of general relativity space time is dynamic. So one could expect that it will not be an static perfec circle but that it will be subject to fluctuations. But if the guge symmetry really is a reflection of the diffeomorphism invariance of the compactified space and this is subject to fluctuations it can´t be a perfect symmetry. Moreover, group theory is good to describe the state of th symmetry in a given moment. But there is symmetry breaking,and group theory is not good to stdy it´s dynamic. In fact the dynamic of symmetry breaking should be equivalent to the dynamcic of compatification. In fact there are "dictionaries" translating symmetry breaking into D-brane theory language. And there are also ways to see gauge symmetries in terms of branes which go beyond the idea that I explained here. But still I think that the idea aapply. Group theory is ufull to analyze statics. But any internal group theory should be related to a compactifications, and you can use topology to study compactification. And topology is mathematically richer than group theory, so it can let you go further. And the key ingredient of analizying compactifications, or symmetri breakings could be related (or one could nspire in the study of) to the dymanic of topology change in general relativity, and indirectly to whormholes. In fact rolled dimesnions have an asociated casimir effect. Maybe this could be an alternative explanation of the cosmoogical constant, but I don´t see exactly how. By the way, the cassimir effect is anothe rthing topological in characters, as well as the arahano-bhor. And solitons and instantons in gauge theories can be studied by means of topology. Definitivelly I think topology is mre interesting that group theory. And possibly algebraic geometry is necesary to complement topology in some cases.
Afther this post I hope that you will understand why I don´t thnk that Garret-Liisi theoyr could be related to important and deep questions in physics. But of course that is only a tangential point of the post. Ah, the most veterans readers of this blog may answer about "knotted strings". I stil don´t see a clear reason why they couldn´t exist, but I still lack a full understanding of many aspects ofstring theory. Obviously is not the easist thing in the wolrd to understand, but it is interesting, certanly.
One of them is pureley mathemathical, I prefer to study things like homology, cohomology, sheaves, spectral sequences, cobordism, morse theory, K-theory and mostly all the topology in the world than group theory. Group theory, and it´s representations, is more or less always the same, but there are a lot of diferent topological tools, all of them with their own peculiarities.
But maths is not a reason a physician could accept. Well, let´s go to physical motivations. One of the goodnes of topology is to try to decide what interestign things happen when one goes from the local tothe global. For example infixing a gauge for a gauge theory you have that any gauge fixing is local and that you can´t extend it to the whole of the phase space. One consecuence of it is the so called Gribov ambiguity. In fact there is a problem with this. Most topological theories are intended to study finite dimensional manifolds and the phase space of a gauge theory is not one of them, so the path is not straighforward from the topology books to their applications in this problems. For example, the BRST operator of gauge theories certainly has the same characteristics than the external derivative of diferential forms. You can form the de-Rham cohomology with the external derivative, to prove that it is equivalent to another cohomologies and use it as a calculational tool for finite manifolds. BRST is usefull, certainly, to select physical states, but I don´t see in the literature that it would be applied to analize the topology of the infinite dimensional phase space. Fortunately there are other things where topology, in its more straightforward form, is interesting, relativity.
One of the things that I find more interesting in general relativity is the role of topology change. The Einstein equations fix the metric of space-time, but don´t say anything specific about it´s topology. In most conventional problems the topology is somewhat assumed. For example in ths schwarschild solution you are studiying something which is topologicallly R3, or, if there is a black-hole you could doubt about the nature of the singularity and to deciede to excise it. Schwarschild space tie is static so it is not problematic. But wen you have a non static space-time things are more intringuing. At a given "time" you have an hypersurface (the technical key word is "slicing"). The natural questions is to wonder if time evolutions, given from the Einstein equations, could change the topology of that hypersurfaces from one time to another. That is a very mathemathically interesting problem in classical gravity and it is usually studied using cobordisms betwen the hypersurfaces. Cobordism intuitive idea is very easy to understand, you wonder when two given n-manifolds can be the border of another n+1-manifold. If you don´t whant to learn cobordism you simply can go to the results which states the criteria under a objects more best known to physicans, characterisitic classes. The results are that if you don´t impose aditional conditions you actually can have topology changes. But when you impose things such like causality and similars the things are more obscure and probably topology change is forbiden. I must say that even if you understand the detaills of the math involved it is somewhat surprising to try to thnk into the details. Afther all in one point you have a metric for a manifold, and later a metric fo ra diferent manifold. And somewhere in the midle you must have a metric which would be good for limit cases of that manifolds. Try to imagine a two dimensinal cae. For example the traditional idea of the formation of a whormhole. You beguin with a 2 sphere and you go nearing two points of it (think for simplicity of two opposite antipodal, points. In the limit beofore the change to the new topology you would have an sphere with the two antipodal points idetntifieds. Afther that you would have a torus.
Try to think about what´s going on just in the intermediate betwen the two cases. Inmediately before you have two tangent spaces which in the intermediate point must be identified. How to interpretate that physically? For that urpose I guess that topology is not the better tool and that the answer would rely in algebraic geometry. I am actually triying to learn algebraic geometry (beyond the one exposed in string theory books) so I can´t go further into this.
I have said "whormhole". Certainlly there is a lot of literature about them. But what I have readed doesn´t actually says too much about the topology change. For transversabble (minkowskian) wormholes you simple decide based in natural requirements a guess form for the metric. But it is all static, you describe the formed wormhole, not the process of it formation. Some tiem ago wormholes where considered funny curiosities usefull for science fiction tales. With the observation of the acclerated universe the thing has changed. The reason is that the existence of a cosmological constant, or of phanthom energy (another possible cause of the acelerating universe) give to wormholes a different position in physicis. The reason is that transversable womhholes require the existence of energy violating the weak energy condition. Usually it was thought that alghoutght it was possible to have small amounts of this matter (by means of quantum effects such like the cassimir effect) it was very unlikely to have too much of it. But the acclerated expansion of the universe make svery plausible that this matter exists. For example in the branworld universes you can have five dimensional matter which in five dimesnions doesn´t vilate that condtion but that it seems to do so in four. The main conclusion is that because of many possible realizations womrholes in a acceraated should exist, and that one must try to find a reason to explain why the don´t exist, or, better, to try to search for them. This could be possible, for example, triying to detect "macroscopic monopoles". The reason is that an usula magnetic field in the vecinity of a wormhole could appear as a magnetic monopole for some observers. Semengly there are concrete proposals for searching them, but I am not totally sure about how the are evolving.
By the way, note that I have said that wormholes are being heavilly studied in the braneworld scenaries. This is one of the reasons I have studied more in deep the Horava-Witten models. I didn´t feel confortable by only understandin the phenomemological approach. In the near future I´ll go back to the study of wormholes, both in conventinoal and in braneworld univeres, and not only to it´s static aspects but to try to understand the dynamics of the formation. If you are a fan of science fiction I can give you a reason why the could be interestings. In SF histories they are usually a tool for interestelar travel or a time machine. But if you think about it if you actually tri to construc a wormhole the most probable thing is that you would connect points that are (very) near one of them. Later you could try to separate the throats of the wormhole. They would be usefull as a fast interstellar travel device only afther you carry the throaths that distance by a conventional way (suposing that the inner distance bethwen the throats doesnt grow). But there is a possible, more realistic, and more usfull way to use a wormhole. You could put one throat near the sun surface and the other near the earth. The solar energy going inside the womrhole will not spread so you will send to the earth the same energy of the sun as the area of the throats. A crude estimation shows that a throat of a few metter of radius will send to the earth the energy that the human the whole race needs. Of course you need to use an intermediate energy vector to use that electromagnetic energy, but that are "minor detaills" xD.
Still one could think that wormholes, or topology change in general relativiey is a too restricitive field. I don´t think so. In string theory there is a great problem. Triying to seek a viable compactification (or going into the landscape if you like that things). But if one thinks a bit about it a compactification is ultimatelly a topology change in the underliying space. Almost all of the work is being done to try to seek for good compactifications. You use a lot of topology and algebraic geometry for that. That is because you study the topology of the resulting space, but you dont wonder how you arrive to that compactificated spaces. String theory goes beyond general relativity, but still it could be interesting to see what a general relativity (or something near to it) could say about that transitions. For example, what kind of matter would inforce that compactifications?
Until nw I have mainly mentioned topology, what about group theory? I am not going to alk too much about it, but, instead, I´ll try to relate it somewhat to compactifications. The easiest place where group theory can appear in quantum physics is in the theory of the angular momentum of a nonreltivistic particle. Rotations in space are described by the SO(3) group. Th universal covering group of SO(3) is SU(2). On the other hand when you have a quantum system with rotational invariane it can be said that, just like in the classical counterpart, the angular momentum is conserved. The classical angular momentum is L=rxp. If you go from the classical momentum p to the quantum operator p you have the definition for the quantum angular momentum. Youcan show that their component´s don´t conmute so you can only observe one of them simultaneously. On the other hand the squared angular momentum L2 conmutes with all the components so you can observe it. You can connec the physics with the group theory saying that L2 is a cassimir operator for a representation, and that you can relate L+- = Lx +- iLy which act as ladder operators, similar to the a+ a- of the harmonic oscilators, to elements of the group theory of SU(2).
This was an external symmetry. Latter, with the advance of particle physics and QFT appeared internal symmetries, and they were related to easy groups. SU(2), SU(3) and U(1). And the first unification attemp was SU(5). The same technicques used for the group theoyr tratement and a few others allowed to do a lot of calculatiions in particle physicis. Another point of group theory was the role played by the poincaré an dLorent group to the classifications of particles. One could relate the spin of a particle to a representations of the Lorentz group. Of course all of this is well known by a lot of the people that wouldmost likely wuld be interested in reading this blog, so which is my point against group theory.
I said that I wuld relate group theory and compactification. Afther all one of the points of stirn gtheory is to recover the ideas of Kaluza-klein. One can show (I did a post, in spanish, in this blog about it) that an five dimensional space compactified in a circle makes that the "external" gravitational of the five dimension becomes an U(1) "internal" simmetyr equivalent to electromagnetism. This is the ideal case. But nature is not allways ideal. In facto it usually isn´t. The hidrogen atom is almost perfectly shperically symmetric, but because of electron, electron-interaction other atoms are not. Still angular momentum is a very usefull quantity, but it doesntt any more is related to a perfect "reall" symmetry.
What about the circle of the compactification?. On could expect that it would be a perfect circle. Afther all symmetric configurations are commonly the right solutions for optimization problems. But if we think in the possible dynamic of the compactification one realize that that circle still i space-time, and because of general relativity space time is dynamic. So one could expect that it will not be an static perfec circle but that it will be subject to fluctuations. But if the guge symmetry really is a reflection of the diffeomorphism invariance of the compactified space and this is subject to fluctuations it can´t be a perfect symmetry. Moreover, group theory is good to describe the state of th symmetry in a given moment. But there is symmetry breaking,and group theory is not good to stdy it´s dynamic. In fact the dynamic of symmetry breaking should be equivalent to the dynamcic of compatification. In fact there are "dictionaries" translating symmetry breaking into D-brane theory language. And there are also ways to see gauge symmetries in terms of branes which go beyond the idea that I explained here. But still I think that the idea aapply. Group theory is ufull to analyze statics. But any internal group theory should be related to a compactifications, and you can use topology to study compactification. And topology is mathematically richer than group theory, so it can let you go further. And the key ingredient of analizying compactifications, or symmetri breakings could be related (or one could nspire in the study of) to the dymanic of topology change in general relativity, and indirectly to whormholes. In fact rolled dimesnions have an asociated casimir effect. Maybe this could be an alternative explanation of the cosmoogical constant, but I don´t see exactly how. By the way, the cassimir effect is anothe rthing topological in characters, as well as the arahano-bhor. And solitons and instantons in gauge theories can be studied by means of topology. Definitivelly I think topology is mre interesting that group theory. And possibly algebraic geometry is necesary to complement topology in some cases.
Afther this post I hope that you will understand why I don´t thnk that Garret-Liisi theoyr could be related to important and deep questions in physics. But of course that is only a tangential point of the post. Ah, the most veterans readers of this blog may answer about "knotted strings". I stil don´t see a clear reason why they couldn´t exist, but I still lack a full understanding of many aspects ofstring theory. Obviously is not the easist thing in the wolrd to understand, but it is interesting, certanly.
Etiquetas:
group theory,
string theory.,
topolgy
Thursday, November 22, 2007
Exceptionally an entry about Garrett Lisi´s ToE
I was aware of the existence of this theory since the post of Lisi in the Sabbines Hosfander "inspirational series". There he stated that "he was cooking a theory to kick the string theory ass" (or something quite similar). Not too surprisingly in the comments sectionhe was quilified by Lubos Motl as an crank.
I am not a terrible fan of group theory and this proposal of ToE (theory of everything) relies heavilly on it. Worst, it depends on E(8). Almost all my knowledge of E(8) comes from the appendix to chapter 6 of Green-Schwartz-Witten book on string theory and from the corresponding entry on wikipedia. More important than this is that it is hard to conceive that it could be possible to gain any insighth in quantum gravity by means of group theory. I mean, gravity is about diferentail geometry, maybe topology. At most it could be thought that gravity is about fibre theory with S0(3,1). Moreover, the Colleman-Mandella theorem states that it is impossible to join the gauge groups and the Lorentz group into a greater group. Everybody having studied supersymmetry knows this anyway (because supergravity scapes this no-go theorem). This is the first objection which Lubos made to the paper when he did his comment (you can read it here).
Garrett replied to that objection in a thread about his theory that is beeing discused at physics forums, concretely this . To be honest I didn´t follow this thread beyod the second page, but I am sure that a lot of information can be found there, as well as the correponding entries in the blos of Sabine Hossfander and Peter Woit (in spanish you could try the one in Migui's Forum.
With so many discusions going there I badly can say anything specially interesting. I find more encouraging the papers about the proof of the Maldacena correspondence (not conjecture any more) or one stating that type II A flux models (closelly related to some kind of braneworld scenaries) are not viable because of the lack of inflation.
So, why an entry about this topic afther all? The main reason is some blogs attacking Garrett Lisi´s not because his theory but because ¡he is a surfer!. Aparently the fact that he works teaching surf and snowboard is enoguth for this people to disqualify a theory. First, this is not the whole history. Lisi is financied by some organization named FQXI. Second, and most important, he seems to have contact with important people in the LQG community (which of course have given a warm wellcome to the theory and are wondering about intergrting it in an spin faom model). Also it is important to state that Lisis has a PhD in physics. All that is much more that Einstein had when he did his five famous contributions to physics in his "anni mirabiliies". But it is not a question of haveing "contacts". The point is that better or worst Garret has an original theory coherently presented in an standard way. Some of the ciritics of his work in the blogosfere have not some mayor contribution to physicis, and it is very unlikely that they could make something beyond very conventional and irrelevant contributions. For sure they are not going to ever make a paper which would get a tiny part of the(deserved or not) impact of lisis´s theory. If Lubos decides to say that Lisis is a crackpot he has behind him a couple of good papers in string theory, and a wonderfull blog with a lot of info in string theory (among other more questionable subjects). And he always would argue using physics (althought he can twist a bit some arguments xD). But his , imitators?, simply have not the authority to be so displicents about this questions.
Once I decided to make a post about the theory I did a quick reading of the paper. He beguins doing a brief summary about basic facts of the standard model and about lie groups theory. In that aspects it looks somehat more like a thesis article than a conventional review article. The fun of this is that it makesit accesible to a broad audiency. Afther a lot of statements relating group theory objects and particles of the standard model (and a few other which should be oberved in the future LHC is his theory is correct) he ends up with an action. The action takes the form of a BF theory, the best friend of the "spin foamers". I am surpried because I would expect gravity arising in a totally diferent way, and it makes me hard to see how unification could arise if gravity relises into this theory. But I guess that this question, and many others, would be addressed in the links that I gave about so I invite to my eventual readers to search there.
A last link, to another blogger talking about this theory. the one in U-duality. He talks about similtudes of this theory with something called homnogeneous supergravity, and possiby with topological string theory. Don't ask me why, but seems that not all string theorist are so negative about Lisi as Lubos. If I would have to give a recomendation about the paper it would be this. It seems to be an entertaining way to learn a bit about E(8), which plays an important role in some aspects of string theory.
O.K. I did this "obligatory" entry. Could you please separate that gun from my head? :P.
Update:
Jacket Distler also has finally made a post about the theory, you can read it here
I find it particularly interesting, as well as the discusion following, in which Garrett appears. Jackes identifies a weak point in the maths, and Garret agree, that if not overcomed would mean that the theory is useless, or more properly said, inconsistent, even at the classical level inwhich it is formulated. Well, as I said before, still the paper could be usefull as an introduction to E(8).
I am not a terrible fan of group theory and this proposal of ToE (theory of everything) relies heavilly on it. Worst, it depends on E(8). Almost all my knowledge of E(8) comes from the appendix to chapter 6 of Green-Schwartz-Witten book on string theory and from the corresponding entry on wikipedia. More important than this is that it is hard to conceive that it could be possible to gain any insighth in quantum gravity by means of group theory. I mean, gravity is about diferentail geometry, maybe topology. At most it could be thought that gravity is about fibre theory with S0(3,1). Moreover, the Colleman-Mandella theorem states that it is impossible to join the gauge groups and the Lorentz group into a greater group. Everybody having studied supersymmetry knows this anyway (because supergravity scapes this no-go theorem). This is the first objection which Lubos made to the paper when he did his comment (you can read it here).
Garrett replied to that objection in a thread about his theory that is beeing discused at physics forums, concretely this . To be honest I didn´t follow this thread beyod the second page, but I am sure that a lot of information can be found there, as well as the correponding entries in the blos of Sabine Hossfander and Peter Woit (in spanish you could try the one in Migui's Forum.
With so many discusions going there I badly can say anything specially interesting. I find more encouraging the papers about the proof of the Maldacena correspondence (not conjecture any more) or one stating that type II A flux models (closelly related to some kind of braneworld scenaries) are not viable because of the lack of inflation.
So, why an entry about this topic afther all? The main reason is some blogs attacking Garrett Lisi´s not because his theory but because ¡he is a surfer!. Aparently the fact that he works teaching surf and snowboard is enoguth for this people to disqualify a theory. First, this is not the whole history. Lisi is financied by some organization named FQXI. Second, and most important, he seems to have contact with important people in the LQG community (which of course have given a warm wellcome to the theory and are wondering about intergrting it in an spin faom model). Also it is important to state that Lisis has a PhD in physics. All that is much more that Einstein had when he did his five famous contributions to physics in his "anni mirabiliies". But it is not a question of haveing "contacts". The point is that better or worst Garret has an original theory coherently presented in an standard way. Some of the ciritics of his work in the blogosfere have not some mayor contribution to physicis, and it is very unlikely that they could make something beyond very conventional and irrelevant contributions. For sure they are not going to ever make a paper which would get a tiny part of the(deserved or not) impact of lisis´s theory. If Lubos decides to say that Lisis is a crackpot he has behind him a couple of good papers in string theory, and a wonderfull blog with a lot of info in string theory (among other more questionable subjects). And he always would argue using physics (althought he can twist a bit some arguments xD). But his , imitators?, simply have not the authority to be so displicents about this questions.
Once I decided to make a post about the theory I did a quick reading of the paper. He beguins doing a brief summary about basic facts of the standard model and about lie groups theory. In that aspects it looks somehat more like a thesis article than a conventional review article. The fun of this is that it makesit accesible to a broad audiency. Afther a lot of statements relating group theory objects and particles of the standard model (and a few other which should be oberved in the future LHC is his theory is correct) he ends up with an action. The action takes the form of a BF theory, the best friend of the "spin foamers". I am surpried because I would expect gravity arising in a totally diferent way, and it makes me hard to see how unification could arise if gravity relises into this theory. But I guess that this question, and many others, would be addressed in the links that I gave about so I invite to my eventual readers to search there.
A last link, to another blogger talking about this theory. the one in U-duality. He talks about similtudes of this theory with something called homnogeneous supergravity, and possiby with topological string theory. Don't ask me why, but seems that not all string theorist are so negative about Lisi as Lubos. If I would have to give a recomendation about the paper it would be this. It seems to be an entertaining way to learn a bit about E(8), which plays an important role in some aspects of string theory.
O.K. I did this "obligatory" entry. Could you please separate that gun from my head? :P.
Update:
Jacket Distler also has finally made a post about the theory, you can read it here
I find it particularly interesting, as well as the discusion following, in which Garrett appears. Jackes identifies a weak point in the maths, and Garret agree, that if not overcomed would mean that the theory is useless, or more properly said, inconsistent, even at the classical level inwhich it is formulated. Well, as I said before, still the paper could be usefull as an introduction to E(8).
Thursday, November 08, 2007
Brane world scenaries and their stringy/M-theory realizations
I bet that among the "vocabulary" of string theory the two that more broadly have expanded in the layman are "Calabi-Yau" and "warped (or brane world) universes". I have already made (in Spanish) a brie introduction to compactifications and Calabi-Yaus. Now I am going to talk about the warped universes and related questions.
I dón´t know the details of the history, but the "heuristic" aspects are clear. After the second string revolution there were two mayor new ingredients in string theory, D-Branes and M-Theory. D-Branes allows the picture of vectorial guage particles trapped in a brane while gravity (.i.e. gravitons) being able to escape the brane and exploring the extra dimensions. This wouldn´t be so important without M-theory. M-Theory lives in 11 dimensions, instead of the superstrings who live in 10 and the nature of the 11th dimensions is somewhat different to that of the 6 extra dimensions of superstrings. In particular it is reasonable to expect that it´s size could be greater than the (Calabi-Yau, or similar) compactified dimensions of the superstrings.
The "natural" scenario seems clear. The universe could be a D3-Brane with the standard model attached to it. The particles of the standard model would be related to a "Calabi-Yau" compactification of 6 of the additional dimensions to a planckanian size and we still have an aditional dimensiosn whose size is not constrained to be planckanian. How great could actually be?.
Well, in the late nineties Arkanni-Hammed, Savas Dimopulus and Dvalli analyzed the question in an a very simple and general framework. They proposed that we would live in a D3-brane and that all other dimensions could be macroscopic and only accessible to gravity. This trivially implied that to short distances Newtonian gravity should be modified so that it would have an 1/R2 + n behaviour, being n the number of additional macroscopic dimensions, instead of the usual, with n=0. The implications of this new behaviour would be that at short distances gravity would be more intense. Surprisingly at that time gravity hadn´t been measured at short distances and the bounds for the distances where the extra dimensions would appear were as great as a millimetre. Soon a few experiments were realized and new bounds arrived. I am not totally sure, but nowadays the allowed size is on the order of at most a decimal of a millimetre. Also it has been discarded (or at least is very unlikely) that more than an additional dimension would be macroscopic (in the sense of non Planckanian).
This ADD scenario was certainly very naive. But the idea of an extra macroscopic deserved further attention. Two different ways to approach it appeared. A phenomenological one the Randall-Sundrum brane world models, and purely string theoretic one, the Horava-Witten theory which realised the idea of heterotic M-theory. I will begin discussing the first ones.
Lisa Randall and Cundrum Sumdrum proposed an scenario where gravity was prevented from "leaking" in the extra dimension was a curvature effect (a warped compactification). They proposed a metric of the form:
1.
Here x represent the coordinates of the usual 4 dimensions and y is the additional dimension. It is assumed that the four dimensional brane is the boundary of a bulk which is a portion of an AdS5 geometry. (this also allow to relate the Randall-Sundrum sceneries to the AdS/CFT correspondence, which, incidentally, has been proved in a very recent, yesterday when this is being written, paper, available here). The parameter l in the metric of the previous equation would be the curvature of that AdS space.
The exponential factor of the metric is responsible of confining gravity. The reason behind the y being in modulus is that we are in an scenario with two branes. One of this correspond to the visible world, the other is a "hidden" brane (usually called also the planck brane). The branes are postioned at y=0 and y=L and there is a Z2-symmetry identification y <-> -y, y+L <->L-y. This relates, at least conceptually, this scenario to the Horava-Witten, as it will be shown later.
From this departure there are two models. The RS-2 model keeps the distance between branes finite. The RS-1 model sends the hidden brane to infinity (i.e. L->infinity) and it effectively behaves as if it would only have one brane. It is the bes suited for being related to AdS/CFT correspondence and an string realization based on flux (warped) compactifications of Type II B superstrings (ore Type II A related to them by mirror symmetry). There are however a few characteristics that this models share. One of them is that they solve the "hierarchy problem". Loosely speaking this problem consists in that the large difference of energy between the electroweak scale and the planck scale requires a very fine tunning of many constants. Supersimmetry could be a solution for this problem, but the Randall-sundrum models solve it in a different way. It can be shown that the energy of the particles in the planck brane is seen in the visible sector damped by the exponential factor of the metric. This automatically addresses the problem. This was, seemingly, the major goal of the first papers in the subject. This explains that the branes are plane Minkowsky space. This means that model is not a cosmologicla model. But there are possible additions which allows to convert it into a cosmological model, let´s say a few about it.
One thing that one would care about going into cosmological considerations is the cosmological constant. It can be seems that the visible brane has a positive tension (understood as self-gravity; in an "stringy" viewpoint it would be the brane tension, i.e. density of energy) while the hidden brane has a negative tension. The bulk, being a AdS, has a negative cosmological constant. The tensions of the branes compensate so the visible brane has a 0 cosmological constant. Introducing matter in the bulk it can get an small positive cosmological constant, but that requires a lot of fine tuning.
The inclusion of matter opens new perspectives. If we must go to a cosmological model we must have matter, and get an FRW scenario (to begin with). The inclusion of matter in this phenomenological model has a curious feature The standard model matter is confined to the branes by a delta function (which certainly is not a "first principles" way to proceed, but, ey it is a phenomenological model). I´ll not dwell into the details (you can find them, for example, in the article that Roy Marteens wrote in the subject for living reviews in relativity, available in the links section of this blog).I´ll simple state that it is actually possible to get an FRW metric.
My main interest here is to present the interplay between this "warped worlds) and string theory, but I can´t avoid to say a few things about two more characteristics of them. The two things are related to black holes.
The first, and most famous, is that the increase of gravity intensity for small distances own to the additional macroscopic dimension. This means that the threesold for the production of a black hole in a collision of particles is seriously reduced. In particular there is an small possibility that in the energy available to the LHC microblack holes could formate (and later evaporate by Hawking process). In fact in the Strings 2007 conferences Lisa-Randall was actually pessimistic about this possibility, but still there is an small window for it.
The other black hole issue is that the rate of evaporation of primordial black holes is modified, actually slowed down. by the extra dimension. In particular that means that most of the primordial black holes wouldn’t have evaporated (that explain why the gamma ray bust corresponding to the last moments of their existence have not been observed) and that the density of that black holes would be high (the probability of being one in the solar system being reasonably high). I must say that the mathematical description of a black hole in the brane worlds is a delicate issue and that it requires numerical calculations.
After heaving done a description of some aspects of the brane world universes let’s go to the Horava Witten theory. It consists of two steps. First one compatifies the theory in a S1/Z(2) orbifold. Such and orbifold is a circle with the upper and inferior half identified that is, a segment. The extremes of the segment are fixed points under the action of the Z(2) group. This means that we have two ten dimensional plains and a 11 dimensional bulk. Requirements of cancellation of gravitational and gauge anomalies in the two orbifold plains require that they must implement an E(8)xE(8)symmetry, the same that most phenomenologically promising heterotic superstring theories. The ten dimensional planes must, actually, compactified into planck sized spaces (usually Calabi-Yaus). The details of the calculations involving anomalies predict a relation between the gauge coupling and the size of the eleventh dimension of the form:
2
Restrictions from cosmology imply that the size of the orbifold would be of the oorder of 10 times the planck size. This is a mayor departure form the RS models. Another thing is that the bulk, would, at least in the simplest models, supersymmetric, i.e. not AdS. Going beyond the "heuristic" description and getting actual effective equations for the model is not a trivial task, but it has been realized. From those equations it is possible to calculate which matter is actually available in the model. And one should try to get a FRW model from them. Well, one can get a hubble era with relativistic matter (i.e. matter at relativistic velocities) but it is now allowed to get non relativistic matter. In fact if one allows some modifications of the model, for example including M5 branes in the bulk, or similar nonperturbative effects to the low energy equations of motion, it could, perhaps, be possible to actually get non relativistic matter in the branes (I am not totally sure of which is the "last day" status of the question because most of the reviews that I have read in this topic are at most from the 2005).
I didn´t present all the details (it would be impossible in a blog sized post) but it is clear that although similar the RS models and the Horava Witten don´t fit totally. This has lead to different lines of research.. On one side there are the Stiendard-Turok Ekpyroctic model. This realizes, at least it is what they claims, very closely the Horava Witten model, but with a very significant diference. Instead of purchasing a FRW model they propose a ciclic model. They propose that form tiem to time (actually thousands mof millions of years) an M5 (or something similar) brane forms in the bulkd and is atracted towards the visible brane, where it desintegrtes resulting in a great increment of the energy which resembles similarities with an expanding universe but actually consist of separation of the particles (and creation of new ones own to the available energy). I didn´t read too much of this model so I can´t say much ore than this.
The other approach is to try to "enginer" RS scenaries form other tools of string theoy. For example one can do wrapped compactifications, as I mentioned at the begining. In that constrcuctioins the visible brane could be an stack of coincident branes. But not necessarilly D3-branes. They could be, for exampled, Dm-branes wraped around n dimesnional "supersymmetric" homological cicles of the compactifeid dimension (which result in a flux) or another constructions.The AdS/CFT correspondence that I have mentiones ocassionaly rquieres the existence (betwen the planck and the standard model branes) of a region many AdS radii in size.The RS sndrum scenario would be the strong coupling version of an older idea for solving the hierarchy problem. One startswith some ultraviolete fixed point CFT around the UV scale (planck scale) and perturbs it by a marginally relevant operator (whose is dimension is close to, say, 4 - ε) then one can naturally generate scales much lower than Mpl. The RG (renormalization group) runningof the couplings in the perturbed field theory is logaritmic, and therefore the relevant coupling will have sgnificant dynamical effects only afther a vast amount of RG running. The translation of this scenario to the RS models is via the AdS/CFT dictionary.
Describing, even "bloglike" the detaills would require another post. But I hope that with what I have told here the reader could get an overview of how goes the interplay betwen phenomenological models and more microscopic stringy considerations.
As a finall comment to sy that not all the string theorist are to conveiced that these secenaries are the most probably realized by nature. Neither it is probable that they would shide light into more fundamental problems of string theory. But what is clear that they have many intriguing posibilties, some of them which could connect to measurable effects and that it is reasonable that people work on them.
I dón´t know the details of the history, but the "heuristic" aspects are clear. After the second string revolution there were two mayor new ingredients in string theory, D-Branes and M-Theory. D-Branes allows the picture of vectorial guage particles trapped in a brane while gravity (.i.e. gravitons) being able to escape the brane and exploring the extra dimensions. This wouldn´t be so important without M-theory. M-Theory lives in 11 dimensions, instead of the superstrings who live in 10 and the nature of the 11th dimensions is somewhat different to that of the 6 extra dimensions of superstrings. In particular it is reasonable to expect that it´s size could be greater than the (Calabi-Yau, or similar) compactified dimensions of the superstrings.
The "natural" scenario seems clear. The universe could be a D3-Brane with the standard model attached to it. The particles of the standard model would be related to a "Calabi-Yau" compactification of 6 of the additional dimensions to a planckanian size and we still have an aditional dimensiosn whose size is not constrained to be planckanian. How great could actually be?.
Well, in the late nineties Arkanni-Hammed, Savas Dimopulus and Dvalli analyzed the question in an a very simple and general framework. They proposed that we would live in a D3-brane and that all other dimensions could be macroscopic and only accessible to gravity. This trivially implied that to short distances Newtonian gravity should be modified so that it would have an 1/R2 + n behaviour, being n the number of additional macroscopic dimensions, instead of the usual, with n=0. The implications of this new behaviour would be that at short distances gravity would be more intense. Surprisingly at that time gravity hadn´t been measured at short distances and the bounds for the distances where the extra dimensions would appear were as great as a millimetre. Soon a few experiments were realized and new bounds arrived. I am not totally sure, but nowadays the allowed size is on the order of at most a decimal of a millimetre. Also it has been discarded (or at least is very unlikely) that more than an additional dimension would be macroscopic (in the sense of non Planckanian).
This ADD scenario was certainly very naive. But the idea of an extra macroscopic deserved further attention. Two different ways to approach it appeared. A phenomenological one the Randall-Sundrum brane world models, and purely string theoretic one, the Horava-Witten theory which realised the idea of heterotic M-theory. I will begin discussing the first ones.
Lisa Randall and Cundrum Sumdrum proposed an scenario where gravity was prevented from "leaking" in the extra dimension was a curvature effect (a warped compactification). They proposed a metric of the form:
1.
Here x represent the coordinates of the usual 4 dimensions and y is the additional dimension. It is assumed that the four dimensional brane is the boundary of a bulk which is a portion of an AdS5 geometry. (this also allow to relate the Randall-Sundrum sceneries to the AdS/CFT correspondence, which, incidentally, has been proved in a very recent, yesterday when this is being written, paper, available here). The parameter l in the metric of the previous equation would be the curvature of that AdS space.
The exponential factor of the metric is responsible of confining gravity. The reason behind the y being in modulus is that we are in an scenario with two branes. One of this correspond to the visible world, the other is a "hidden" brane (usually called also the planck brane). The branes are postioned at y=0 and y=L and there is a Z2-symmetry identification y <-> -y, y+L <->L-y. This relates, at least conceptually, this scenario to the Horava-Witten, as it will be shown later.
From this departure there are two models. The RS-2 model keeps the distance between branes finite. The RS-1 model sends the hidden brane to infinity (i.e. L->infinity) and it effectively behaves as if it would only have one brane. It is the bes suited for being related to AdS/CFT correspondence and an string realization based on flux (warped) compactifications of Type II B superstrings (ore Type II A related to them by mirror symmetry). There are however a few characteristics that this models share. One of them is that they solve the "hierarchy problem". Loosely speaking this problem consists in that the large difference of energy between the electroweak scale and the planck scale requires a very fine tunning of many constants. Supersimmetry could be a solution for this problem, but the Randall-sundrum models solve it in a different way. It can be shown that the energy of the particles in the planck brane is seen in the visible sector damped by the exponential factor of the metric. This automatically addresses the problem. This was, seemingly, the major goal of the first papers in the subject. This explains that the branes are plane Minkowsky space. This means that model is not a cosmologicla model. But there are possible additions which allows to convert it into a cosmological model, let´s say a few about it.
One thing that one would care about going into cosmological considerations is the cosmological constant. It can be seems that the visible brane has a positive tension (understood as self-gravity; in an "stringy" viewpoint it would be the brane tension, i.e. density of energy) while the hidden brane has a negative tension. The bulk, being a AdS, has a negative cosmological constant. The tensions of the branes compensate so the visible brane has a 0 cosmological constant. Introducing matter in the bulk it can get an small positive cosmological constant, but that requires a lot of fine tuning.
The inclusion of matter opens new perspectives. If we must go to a cosmological model we must have matter, and get an FRW scenario (to begin with). The inclusion of matter in this phenomenological model has a curious feature The standard model matter is confined to the branes by a delta function (which certainly is not a "first principles" way to proceed, but, ey it is a phenomenological model). I´ll not dwell into the details (you can find them, for example, in the article that Roy Marteens wrote in the subject for living reviews in relativity, available in the links section of this blog).I´ll simple state that it is actually possible to get an FRW metric.
My main interest here is to present the interplay between this "warped worlds) and string theory, but I can´t avoid to say a few things about two more characteristics of them. The two things are related to black holes.
The first, and most famous, is that the increase of gravity intensity for small distances own to the additional macroscopic dimension. This means that the threesold for the production of a black hole in a collision of particles is seriously reduced. In particular there is an small possibility that in the energy available to the LHC microblack holes could formate (and later evaporate by Hawking process). In fact in the Strings 2007 conferences Lisa-Randall was actually pessimistic about this possibility, but still there is an small window for it.
The other black hole issue is that the rate of evaporation of primordial black holes is modified, actually slowed down. by the extra dimension. In particular that means that most of the primordial black holes wouldn’t have evaporated (that explain why the gamma ray bust corresponding to the last moments of their existence have not been observed) and that the density of that black holes would be high (the probability of being one in the solar system being reasonably high). I must say that the mathematical description of a black hole in the brane worlds is a delicate issue and that it requires numerical calculations.
After heaving done a description of some aspects of the brane world universes let’s go to the Horava Witten theory. It consists of two steps. First one compatifies the theory in a S1/Z(2) orbifold. Such and orbifold is a circle with the upper and inferior half identified that is, a segment. The extremes of the segment are fixed points under the action of the Z(2) group. This means that we have two ten dimensional plains and a 11 dimensional bulk. Requirements of cancellation of gravitational and gauge anomalies in the two orbifold plains require that they must implement an E(8)xE(8)symmetry, the same that most phenomenologically promising heterotic superstring theories. The ten dimensional planes must, actually, compactified into planck sized spaces (usually Calabi-Yaus). The details of the calculations involving anomalies predict a relation between the gauge coupling and the size of the eleventh dimension of the form:
2
Restrictions from cosmology imply that the size of the orbifold would be of the oorder of 10 times the planck size. This is a mayor departure form the RS models. Another thing is that the bulk, would, at least in the simplest models, supersymmetric, i.e. not AdS. Going beyond the "heuristic" description and getting actual effective equations for the model is not a trivial task, but it has been realized. From those equations it is possible to calculate which matter is actually available in the model. And one should try to get a FRW model from them. Well, one can get a hubble era with relativistic matter (i.e. matter at relativistic velocities) but it is now allowed to get non relativistic matter. In fact if one allows some modifications of the model, for example including M5 branes in the bulk, or similar nonperturbative effects to the low energy equations of motion, it could, perhaps, be possible to actually get non relativistic matter in the branes (I am not totally sure of which is the "last day" status of the question because most of the reviews that I have read in this topic are at most from the 2005).
I didn´t present all the details (it would be impossible in a blog sized post) but it is clear that although similar the RS models and the Horava Witten don´t fit totally. This has lead to different lines of research.. On one side there are the Stiendard-Turok Ekpyroctic model. This realizes, at least it is what they claims, very closely the Horava Witten model, but with a very significant diference. Instead of purchasing a FRW model they propose a ciclic model. They propose that form tiem to time (actually thousands mof millions of years) an M5 (or something similar) brane forms in the bulkd and is atracted towards the visible brane, where it desintegrtes resulting in a great increment of the energy which resembles similarities with an expanding universe but actually consist of separation of the particles (and creation of new ones own to the available energy). I didn´t read too much of this model so I can´t say much ore than this.
The other approach is to try to "enginer" RS scenaries form other tools of string theoy. For example one can do wrapped compactifications, as I mentioned at the begining. In that constrcuctioins the visible brane could be an stack of coincident branes. But not necessarilly D3-branes. They could be, for exampled, Dm-branes wraped around n dimesnional "supersymmetric" homological cicles of the compactifeid dimension (which result in a flux) or another constructions.The AdS/CFT correspondence that I have mentiones ocassionaly rquieres the existence (betwen the planck and the standard model branes) of a region many AdS radii in size.The RS sndrum scenario would be the strong coupling version of an older idea for solving the hierarchy problem. One startswith some ultraviolete fixed point CFT around the UV scale (planck scale) and perturbs it by a marginally relevant operator (whose is dimension is close to, say, 4 - ε) then one can naturally generate scales much lower than Mpl. The RG (renormalization group) runningof the couplings in the perturbed field theory is logaritmic, and therefore the relevant coupling will have sgnificant dynamical effects only afther a vast amount of RG running. The translation of this scenario to the RS models is via the AdS/CFT dictionary.
Describing, even "bloglike" the detaills would require another post. But I hope that with what I have told here the reader could get an overview of how goes the interplay betwen phenomenological models and more microscopic stringy considerations.
As a finall comment to sy that not all the string theorist are to conveiced that these secenaries are the most probably realized by nature. Neither it is probable that they would shide light into more fundamental problems of string theory. But what is clear that they have many intriguing posibilties, some of them which could connect to measurable effects and that it is reasonable that people work on them.
Wednesday, November 07, 2007
Renormalizable ma non troppo
My intention for this post was to make an exposition of Horava-Witten theory and the phenomenological and cosmological theories related to them (brane universes, ekptyroptic, etc).
But a confluence of factors has decided me to make a brief post about a diferent topic. In a previous entry I talked about conformal gravity. That was a nice theory which could presumably reproduce general relativity in the appropiate limits, and it was renormalizable. I haven´t head nothing new about it since that post, but I neither have had time to search so maybe there is something going on and simply a am not aware of it.
Since them I have had notice of ¡3! diferent claims about new viable paths to quantum gravity. I´ll explain a bit about them.
The first is the effort of Martin Reuter in triying to prove that classical pure (i.e. no matter) general relativity can have an UV fixed point. I am not still very expert in the insights of Wilson and Polchinsky in the renormalization group, but the idea goes as follows. In any QFT loops usually give rise to infinite terms. To get around them you do a cutt-off and you separate the integral in a finte and an infinte part. Them you add a new term to the lagraingian (a counterterm) which generates an aditional diagram whcih cancels the divergent part of the integral. Inthis way ou can deal with any theory, renormalizable or not. But in renormalizable theories the counterterms have the same form as the original terms of the lagrangian so you can cancel the divergences by apropiate redefinitions of parameters of the lagrangian (coupling constants, masses, wavefunctions, etc). If the neccessary counterterms are not of the same form that the orignial lagrangian this resoults into the adition of new parameters of the theory. You can have by this procedure a finite theory,, but with an infinite number of free parameters, i.e., with no predicitive power. General relativity is of this type. But there is a possible scape to this problem. It could be that there are aditional aspects which constraint the values of all that necessary infinte number of parameters so all of them have the same value and the predictive power of the theory is recovered. Theories with such behaviour are said to have an UV (ultra violete) fixed point. (Wilson-Polchinsky renormalization group theory consist in many other aspects, but this is all I need of renormalization group theory to explain what´s going on here).
Martin Reuter is triying to probe that pure general relativy actually has an UV fixed point. To do so he must do some desompositoins which allow to do some numerical analisys. The results of the numerical analisys strongly suggest the existence of the UV fixed point. He also can uses that results to get some results incosmology. I havent readed too mcuh about the details so I´ll not say anything about them. What I must say is that there is a problem with all this. If matter is added to the theory it can be shown that you are adding wht are called relevant operators and that you will go out of the UV fixed point so semmengly all that effort would be poinless. In fact some people in LQG (canonical as well as spin foam versions) are triying to recover matter as some kind of topological deffects, or other, very bizarre, constructons out of pure gravity. If they would be succesfull ther would be no need to add matter and the UV fixed point would be kept. That would be very good for them because the wouold have on one hand a way to do perturbative quantum gravity from conventional Einstein gravity and on the other hand a non perturbative formulation which allows them to prove things about diferent interesting questions (pity that they don´t know how to recover conventional gerneral relativity from that non perturbvative formulation).
Well, very recenly I have had news about a theory made by Krasnov kown as "non metric quantum gravity". You can read about it here.
The presentation sounds very promising. Using Plebansky action (a very familar for LQG people alternative formulation of general relativity equivalent to it, under addecquate constraints, in the classical limit). They quantize it in somethnig resembling the well known background field method . This method was introduced in the fifties by de Witt to obtain for the first time a (quasi)covariant quantization of general relativity which gave a more rigurous tratement of the previous work of Feynman who had obtained Feynman graphs (obvious xD) for general relativity. The theory is based in separating the field to be quantized in two parts, one, the background, is not quantized and only the fuctuations about it are quantized. Ideally the nonquantizd part would be a limit in which the quantum fluctuations of the quantized part are irrelevant. It is interesting thatthis formalism later impulsed the technology wich would allow to quantize yang mills theories (in fact later better ways were found to quantize them and in the QFT textbooks usually there is no reference to the background field method). In fact there is nothing terribly special about the background field method, it is justa diferent way to do perturbative quantization. So one could ask how this would render Plebansky theory renormalizable. The asnwer is ¡it doesn´t !. If you read the article you find that contrary to the claims the theory is not renormalizable. But beofre wondering if you would make a demand to the authros about fake publicity continuate reading -if you have arrived untill here a litle more effort doesn´t matter ;)-. The trick is that they claim that they can prove that the theory has an UV fixed point (yeah, again). The advantage that I see of this aproach over the Reuter´s one is that there are not numerical calculus and artificial algoritmic constructions involved. But still the same drawback applies. They are theories of pure gravity and the UV would dissapear if matter is added (well, I guess it would be so, I cant say for sure).
There are aditional papers exploring the properties of the theory. Seemengly it can explain dark matter, quasars anomalous red shifts and such that. Pitty it can´t explain ordinary, vissible, matter.
If I must decide among these thre theories, conformal gravity, reuters approach, and kranosv non metric gravity I clearly prefer conformal gravity. It is a renormalizbel theory, without need to use fixed points, and it allows the introductoin of matter. I have readed in Jackes Distler blog some claism which maybe would be a problem for this theory, but I am not totally sure about it.
And to end I´ll say a few words about the new baby quantum gravity, or I would better say a TOE (theory of everything). It´s author is Garret Lissi. You can find his paper here. Sabine Hossfander makes a good blog post about it here so I invite to read that entry. I just will quote a phrase of Sabbine:
He neither can say anything about the quantization of gravity, renormalizability, nor about the hierarchy problem
Well, the requirements for a TOE seem to have drop a bit since the last time I watched ;).
Of courseI again reiterate that I don´t consider myself nothin remotely similar to an authority in this questions and that I invite to the reader to form his own conclusions.
But a confluence of factors has decided me to make a brief post about a diferent topic. In a previous entry I talked about conformal gravity. That was a nice theory which could presumably reproduce general relativity in the appropiate limits, and it was renormalizable. I haven´t head nothing new about it since that post, but I neither have had time to search so maybe there is something going on and simply a am not aware of it.
Since them I have had notice of ¡3! diferent claims about new viable paths to quantum gravity. I´ll explain a bit about them.
The first is the effort of Martin Reuter in triying to prove that classical pure (i.e. no matter) general relativity can have an UV fixed point. I am not still very expert in the insights of Wilson and Polchinsky in the renormalization group, but the idea goes as follows. In any QFT loops usually give rise to infinite terms. To get around them you do a cutt-off and you separate the integral in a finte and an infinte part. Them you add a new term to the lagraingian (a counterterm) which generates an aditional diagram whcih cancels the divergent part of the integral. Inthis way ou can deal with any theory, renormalizable or not. But in renormalizable theories the counterterms have the same form as the original terms of the lagrangian so you can cancel the divergences by apropiate redefinitions of parameters of the lagrangian (coupling constants, masses, wavefunctions, etc). If the neccessary counterterms are not of the same form that the orignial lagrangian this resoults into the adition of new parameters of the theory. You can have by this procedure a finite theory,, but with an infinite number of free parameters, i.e., with no predicitive power. General relativity is of this type. But there is a possible scape to this problem. It could be that there are aditional aspects which constraint the values of all that necessary infinte number of parameters so all of them have the same value and the predictive power of the theory is recovered. Theories with such behaviour are said to have an UV (ultra violete) fixed point. (Wilson-Polchinsky renormalization group theory consist in many other aspects, but this is all I need of renormalization group theory to explain what´s going on here).
Martin Reuter is triying to probe that pure general relativy actually has an UV fixed point. To do so he must do some desompositoins which allow to do some numerical analisys. The results of the numerical analisys strongly suggest the existence of the UV fixed point. He also can uses that results to get some results incosmology. I havent readed too mcuh about the details so I´ll not say anything about them. What I must say is that there is a problem with all this. If matter is added to the theory it can be shown that you are adding wht are called relevant operators and that you will go out of the UV fixed point so semmengly all that effort would be poinless. In fact some people in LQG (canonical as well as spin foam versions) are triying to recover matter as some kind of topological deffects, or other, very bizarre, constructons out of pure gravity. If they would be succesfull ther would be no need to add matter and the UV fixed point would be kept. That would be very good for them because the wouold have on one hand a way to do perturbative quantum gravity from conventional Einstein gravity and on the other hand a non perturbative formulation which allows them to prove things about diferent interesting questions (pity that they don´t know how to recover conventional gerneral relativity from that non perturbvative formulation).
Well, very recenly I have had news about a theory made by Krasnov kown as "non metric quantum gravity". You can read about it here.
The presentation sounds very promising. Using Plebansky action (a very familar for LQG people alternative formulation of general relativity equivalent to it, under addecquate constraints, in the classical limit). They quantize it in somethnig resembling the well known background field method . This method was introduced in the fifties by de Witt to obtain for the first time a (quasi)covariant quantization of general relativity which gave a more rigurous tratement of the previous work of Feynman who had obtained Feynman graphs (obvious xD) for general relativity. The theory is based in separating the field to be quantized in two parts, one, the background, is not quantized and only the fuctuations about it are quantized. Ideally the nonquantizd part would be a limit in which the quantum fluctuations of the quantized part are irrelevant. It is interesting thatthis formalism later impulsed the technology wich would allow to quantize yang mills theories (in fact later better ways were found to quantize them and in the QFT textbooks usually there is no reference to the background field method). In fact there is nothing terribly special about the background field method, it is justa diferent way to do perturbative quantization. So one could ask how this would render Plebansky theory renormalizable. The asnwer is ¡it doesn´t !. If you read the article you find that contrary to the claims the theory is not renormalizable. But beofre wondering if you would make a demand to the authros about fake publicity continuate reading -if you have arrived untill here a litle more effort doesn´t matter ;)-. The trick is that they claim that they can prove that the theory has an UV fixed point (yeah, again). The advantage that I see of this aproach over the Reuter´s one is that there are not numerical calculus and artificial algoritmic constructions involved. But still the same drawback applies. They are theories of pure gravity and the UV would dissapear if matter is added (well, I guess it would be so, I cant say for sure).
There are aditional papers exploring the properties of the theory. Seemengly it can explain dark matter, quasars anomalous red shifts and such that. Pitty it can´t explain ordinary, vissible, matter.
If I must decide among these thre theories, conformal gravity, reuters approach, and kranosv non metric gravity I clearly prefer conformal gravity. It is a renormalizbel theory, without need to use fixed points, and it allows the introductoin of matter. I have readed in Jackes Distler blog some claism which maybe would be a problem for this theory, but I am not totally sure about it.
And to end I´ll say a few words about the new baby quantum gravity, or I would better say a TOE (theory of everything). It´s author is Garret Lissi. You can find his paper here. Sabine Hossfander makes a good blog post about it here so I invite to read that entry. I just will quote a phrase of Sabbine:
He neither can say anything about the quantization of gravity, renormalizability, nor about the hierarchy problem
Well, the requirements for a TOE seem to have drop a bit since the last time I watched ;).
Of courseI again reiterate that I don´t consider myself nothin remotely similar to an authority in this questions and that I invite to the reader to form his own conclusions.
Tuesday, November 06, 2007
String dualities and M-Theory
I have changed the name of the blog to somewhat most "stringy" (that is, the possible dimensions of spacetiem in string theories). In fact it also was the usual califications I used to have in exams in a far past (and indded in the very last exam that I did, well, almost), that is, upper the maximum, but unfortunatelly I stopped to get that notes when they could have been more usefull. Anyway, the main reason is that I didnt´like the name of the journal and I neded something diferent, who knows if I´ll keep this name or I´ll change it. Let´s go now with the stuff.
One of the most important discoveries in string theory, the origin of the so called, second revolution, was to realize the fact (or at least to get firm evidence of) that the originally different string theories were in fact different aspects of a single theory. This somewhat remembers me one of the best known fable o Aesops (essopo in Spanish), the blind man and the elephant. There six blind man, presumably smart and knowledge people, had to describe how it was an elephant. One touched first the ear of the animal and said it was like an “bbanico” other touched first the nose (don’t know the English word for "trompa") and said it was like an snake, other touched the, er, "cola" (I really need to install an English Spanish dictionary) and thought that it was an string (obviously this was an string theorist :P) and so on.
Well, in string theory there is a slight analogy with the fable. Initially it was created the bosonic string, which needs 26 dimensions for it’s existence. From the very beginning it was obvious that it was mainly a toy theory. The universe that the physics study has fermions, so it was needed a theory which describes fermions. There were two ways to achieve this. One was introducing additional Grasman anticonmuting variables and writing an analogous of the Green-Schwartz lagrangian of the bosonic string. A different, and more useful for practical calculations, approach was to consider string theory s a theory of fields in the world-sheet (the two dimensional surface which is the evolution of a string). In addition to the bosonic fields X(s) which can be identified with the coordinates of the string, there were additional two dimensional fermionic fields which together formed an supersimetric multiplet. Until now there are some uniqueness, but it soon disappears.
In the bosonic string we have two types, open and closed strings (althought it is belived that a purelly interacting open string is inconsistent, loop diagrams of open strings should be equivalente to tree level closed string diagrams). A closed string comes from imposing periodic conditions to the fields, i.e. X(s + 2phi)=X(s). Well, for the superstring theory similar considerations must be held. Open superstring theoyr is known as Type I string theory. Closed string theory is known as type II.
But thing don´t end here. In adition to the periodic conditions for the bosonic fields you must add some periodicity conditions for the other fields. But for fermions it natural to have periodics as well as antiperiodic conditions. I will not dive into the detailss, but the final result is that you have two kinds of type II superstrings type A and type b.
But the thing doesn´t end there. In the worldsheet you have left moving and right moving fields. In the mid eighties Martinec et all created a new string theory by allowing that the left moving modes would be pure bosnic string theory wheil the left moving would be supersmultiplets. These are known as heterotic string theories. I speak of them in plural becuse there are two of them. You need to impose some conditions in the left moving bosonic fields so that they would result in anomaly free theories (basically that you compactify in an even dual self-latice). This has the consecuence that the heterotic theories are tied to simmety groups resulting from that compactification. The allowed groups are SO(32) and E(8)xE(8). Specially the second one is a very good candidate for unification of the standar model unification.
But with all this we have five consistent theories. That was somewhat ugly. In fact the expectation was the only good candidate to recover the standard model at low energies was the E(8)xE(8) heterotic string (b.t.w. soon afther the initial construction it was realized that you could get it by a diferent aproach, bosnization, which didn´t require that left moving "pure bosnic" modes, which were somewhat antiaestehic). But even so it was annoying to have self consisten theories which seemengly were useless.
The solution came from dualities. The word "duality" must be one of the more overused ones in math andn physic. Loosely speaking you can think that you have a dualitiy when you have diferent (and complementary) descriptions of the same phenomena.
Concretelly in string theory there are thre basic types of dualities. T, S and U duality.
T duality is a perturbative duality. I.e. is valid order by order in perturbation theory. To be honest I doubt that anyone whoe doesn´t know what a perturbaive solution is could be recomendto be reading this post, but anyway I´ll say a few things about it.
In quantum (or classic) mechanics only a few problems can be solved exactly -i.e. analitically-. Even linear problems can´t usually be solved exactlly. Fortunatelly in many practical cases you have that you can aproach the unsovlabel problem by a solvable one. That is you can get a separation of the form:
H=Hs + gHp
Here H is the full hamiltonian (or for what mattter lagrangian, i.e. a function(al) which describes the system. H s is the soluble part g is a constant, tipically small, and Hpis the perturbation hamiltonian. The tactic is to search for solutions of the form:
Φ= Φ0 + gΦ1 + g2Φ2 + ....
That is, you have an infinite power series in the perturbative constant.
in quantum field theory, and for practical purposes, for string theory, Hs is always the ahmiltonina, or more usually lagrangina, for a free theoy, and Hp is tipically an interaction term. The perturbbative coupling is usually a couupling constant which describes the intensity of the interaction (for the coulmb law is the alpha constanct, which is related to the coulmb constant, for gravity it would be a constant related to the newton constant. The notation Φ comes fom the fact that in quantum mechanis the solution of a problem is a wave funtion, there is an perturbation theory fo rclassical mechanics, but i will not say anything about it.
Well, soon we will see why I have introduced these detailsl, but first I´ll explain what T duality is. The easiest ralization of T-duality is the compactification of one of the coordinates of the bosonic string in a circle of radius R. When you do that compactificaton you have that some closed strings can wrap the compactified dimension w times. That is known as the wraping number. Another aspect is thatin the compact dimensions the moment can´t be continous, it must be a discrete number, n.Well, you have that the thoeir compactified in a radius R is equal to a theorie compactified in a radius alpha/R if simultaneowulsy you exchange n and w.
For superstring theories you have similar T-dualities which relates some theories with anothers. But that´s not all the history. IN the mid ninties it was discover that in adition to strings (one dimensinoal objects) string theories needed to have upper dimensional objects whcih I´ll call, generally, p-branes where p indicates the dimensionality of the object. Tipically they will be Dp-branes.
Without going into the detaills, you can find some in this entry, you get that type II A theoir has even dimensinal Dp-Branes and that Type II b has odd dimensinal branes. If you do compactifications you have that in addition to relations betwen stirng related states, some Dp-branes of a theory are equivalent to anothers. As I discused in some previous post compactifications in a circle (or torus) are not realisitic. Some more realisitic compactifications are the Calabi-Yau spaces. There an analogous of T-Duality is cnjectured to exist under the name of mirror symmetry.
But even most important that T-duality is S-duality. This relates a weak coupling perturbative expansion for a theory for an strong coupling, non perturbative expansion of another theory. That is, if you exchange in a perturbative serie the coupling constant of a theory (typically represented by a field known as the dilaton field) by the inverse of the coupling of the other you have the same results. Aditionally you have there relations betwen the Dp-Branes. A particularlly spectacular case is that you can exhcange "fundamental" strings of one theory by D1-branes of the other (just for curiosity comment that the "magnetic" analogous of the tring is an NS5-brane. Well, the NS% brane of a theory is exchanged by a D5 brane of the other).
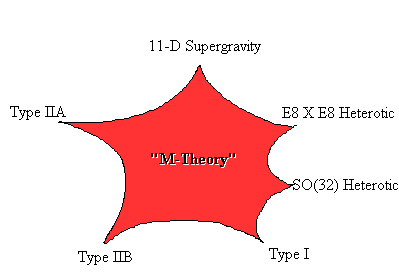
This images shows the web of dualities of string theory.
I have stated the resoults of the dualities, but haven´t said how one arrives to them. There various independent aproachs that give hints about this dualities. One of them is to get a low energy limt of stirng theoy, supergravity theories in the apropiate dimension. A particularllyniteresting thing comes form this.
In type II A theory you have a colection of Do-branes which look like somthing simlilar to what is known as a "kaluza klein tower". This KKT usually is a signal of an aditional dimension. That is, you have an indications of an eleventh dimension. The size of that diemsnion is related to the coupling constant,λ, of the type II A theory by the relation:
R=λ2/3.
There are aditional suport for this relation. For example 11 dimensinal supergravity compactified apropiately is equivalent to the 10 dimensional supergravity which is the low energy limit of type II A string theory.
This 11 dimensional theoy is known as M-Theoy. There is not a precise formulation of it (and it is suspected that it has not a classical limit which allows to give a lagrangian for it). Despite this there are ways to relate it to the other string theories. So the general picture emerging from all this is that there is a single theorie, whcih perturbative form can be described by a theory of fundamental strings. And the diferent limits of it are the known strings.
But not all of the limits are necessrally good candidates to represent the observed universe. Nowadays the most promising candidates are a particular limit of M-Theory which aproachs it to the heterotic strings, known as "heterotic M-theory" and a particular kind of compatifications of Type II theories kown as "lux compactifications. In a next post I-ll talk about the Horave-Witen model (an hterotic M-mtheory realization) whcis is particularly well siuted for phenomenologie and which has inspired well known areas of research such as the Randall-Sundrum models and the Ekppirotyc universe.
One of the most important discoveries in string theory, the origin of the so called, second revolution, was to realize the fact (or at least to get firm evidence of) that the originally different string theories were in fact different aspects of a single theory. This somewhat remembers me one of the best known fable o Aesops (essopo in Spanish), the blind man and the elephant. There six blind man, presumably smart and knowledge people, had to describe how it was an elephant. One touched first the ear of the animal and said it was like an “bbanico” other touched first the nose (don’t know the English word for "trompa") and said it was like an snake, other touched the, er, "cola" (I really need to install an English Spanish dictionary) and thought that it was an string (obviously this was an string theorist :P) and so on.
Well, in string theory there is a slight analogy with the fable. Initially it was created the bosonic string, which needs 26 dimensions for it’s existence. From the very beginning it was obvious that it was mainly a toy theory. The universe that the physics study has fermions, so it was needed a theory which describes fermions. There were two ways to achieve this. One was introducing additional Grasman anticonmuting variables and writing an analogous of the Green-Schwartz lagrangian of the bosonic string. A different, and more useful for practical calculations, approach was to consider string theory s a theory of fields in the world-sheet (the two dimensional surface which is the evolution of a string). In addition to the bosonic fields X(s) which can be identified with the coordinates of the string, there were additional two dimensional fermionic fields which together formed an supersimetric multiplet. Until now there are some uniqueness, but it soon disappears.
In the bosonic string we have two types, open and closed strings (althought it is belived that a purelly interacting open string is inconsistent, loop diagrams of open strings should be equivalente to tree level closed string diagrams). A closed string comes from imposing periodic conditions to the fields, i.e. X(s + 2phi)=X(s). Well, for the superstring theory similar considerations must be held. Open superstring theoyr is known as Type I string theory. Closed string theory is known as type II.
But thing don´t end here. In adition to the periodic conditions for the bosonic fields you must add some periodicity conditions for the other fields. But for fermions it natural to have periodics as well as antiperiodic conditions. I will not dive into the detailss, but the final result is that you have two kinds of type II superstrings type A and type b.
But the thing doesn´t end there. In the worldsheet you have left moving and right moving fields. In the mid eighties Martinec et all created a new string theory by allowing that the left moving modes would be pure bosnic string theory wheil the left moving would be supersmultiplets. These are known as heterotic string theories. I speak of them in plural becuse there are two of them. You need to impose some conditions in the left moving bosonic fields so that they would result in anomaly free theories (basically that you compactify in an even dual self-latice). This has the consecuence that the heterotic theories are tied to simmety groups resulting from that compactification. The allowed groups are SO(32) and E(8)xE(8). Specially the second one is a very good candidate for unification of the standar model unification.
But with all this we have five consistent theories. That was somewhat ugly. In fact the expectation was the only good candidate to recover the standard model at low energies was the E(8)xE(8) heterotic string (b.t.w. soon afther the initial construction it was realized that you could get it by a diferent aproach, bosnization, which didn´t require that left moving "pure bosnic" modes, which were somewhat antiaestehic). But even so it was annoying to have self consisten theories which seemengly were useless.
The solution came from dualities. The word "duality" must be one of the more overused ones in math andn physic. Loosely speaking you can think that you have a dualitiy when you have diferent (and complementary) descriptions of the same phenomena.
Concretelly in string theory there are thre basic types of dualities. T, S and U duality.
T duality is a perturbative duality. I.e. is valid order by order in perturbation theory. To be honest I doubt that anyone whoe doesn´t know what a perturbaive solution is could be recomendto be reading this post, but anyway I´ll say a few things about it.
In quantum (or classic) mechanics only a few problems can be solved exactly -i.e. analitically-. Even linear problems can´t usually be solved exactlly. Fortunatelly in many practical cases you have that you can aproach the unsovlabel problem by a solvable one. That is you can get a separation of the form:
H=Hs + gHp
Here H is the full hamiltonian (or for what mattter lagrangian, i.e. a function(al) which describes the system. H s is the soluble part g is a constant, tipically small, and Hpis the perturbation hamiltonian. The tactic is to search for solutions of the form:
Φ= Φ0 + gΦ1 + g2Φ2 + ....
That is, you have an infinite power series in the perturbative constant.
in quantum field theory, and for practical purposes, for string theory, Hs is always the ahmiltonina, or more usually lagrangina, for a free theoy, and Hp is tipically an interaction term. The perturbbative coupling is usually a couupling constant which describes the intensity of the interaction (for the coulmb law is the alpha constanct, which is related to the coulmb constant, for gravity it would be a constant related to the newton constant. The notation Φ comes fom the fact that in quantum mechanis the solution of a problem is a wave funtion, there is an perturbation theory fo rclassical mechanics, but i will not say anything about it.
Well, soon we will see why I have introduced these detailsl, but first I´ll explain what T duality is. The easiest ralization of T-duality is the compactification of one of the coordinates of the bosonic string in a circle of radius R. When you do that compactificaton you have that some closed strings can wrap the compactified dimension w times. That is known as the wraping number. Another aspect is thatin the compact dimensions the moment can´t be continous, it must be a discrete number, n.Well, you have that the thoeir compactified in a radius R is equal to a theorie compactified in a radius alpha/R if simultaneowulsy you exchange n and w.
For superstring theories you have similar T-dualities which relates some theories with anothers. But that´s not all the history. IN the mid ninties it was discover that in adition to strings (one dimensinoal objects) string theories needed to have upper dimensional objects whcih I´ll call, generally, p-branes where p indicates the dimensionality of the object. Tipically they will be Dp-branes.
Without going into the detaills, you can find some in this entry, you get that type II A theoir has even dimensinal Dp-Branes and that Type II b has odd dimensinal branes. If you do compactifications you have that in addition to relations betwen stirng related states, some Dp-branes of a theory are equivalent to anothers. As I discused in some previous post compactifications in a circle (or torus) are not realisitic. Some more realisitic compactifications are the Calabi-Yau spaces. There an analogous of T-Duality is cnjectured to exist under the name of mirror symmetry.
But even most important that T-duality is S-duality. This relates a weak coupling perturbative expansion for a theory for an strong coupling, non perturbative expansion of another theory. That is, if you exchange in a perturbative serie the coupling constant of a theory (typically represented by a field known as the dilaton field) by the inverse of the coupling of the other you have the same results. Aditionally you have there relations betwen the Dp-Branes. A particularlly spectacular case is that you can exhcange "fundamental" strings of one theory by D1-branes of the other (just for curiosity comment that the "magnetic" analogous of the tring is an NS5-brane. Well, the NS% brane of a theory is exchanged by a D5 brane of the other).

This images shows the web of dualities of string theory.
I have stated the resoults of the dualities, but haven´t said how one arrives to them. There various independent aproachs that give hints about this dualities. One of them is to get a low energy limt of stirng theoy, supergravity theories in the apropiate dimension. A particularllyniteresting thing comes form this.
In type II A theory you have a colection of Do-branes which look like somthing simlilar to what is known as a "kaluza klein tower". This KKT usually is a signal of an aditional dimension. That is, you have an indications of an eleventh dimension. The size of that diemsnion is related to the coupling constant,λ, of the type II A theory by the relation:
R=λ2/3.
There are aditional suport for this relation. For example 11 dimensinal supergravity compactified apropiately is equivalent to the 10 dimensional supergravity which is the low energy limit of type II A string theory.
This 11 dimensional theoy is known as M-Theoy. There is not a precise formulation of it (and it is suspected that it has not a classical limit which allows to give a lagrangian for it). Despite this there are ways to relate it to the other string theories. So the general picture emerging from all this is that there is a single theorie, whcih perturbative form can be described by a theory of fundamental strings. And the diferent limits of it are the known strings.
But not all of the limits are necessrally good candidates to represent the observed universe. Nowadays the most promising candidates are a particular limit of M-Theory which aproachs it to the heterotic strings, known as "heterotic M-theory" and a particular kind of compatifications of Type II theories kown as "lux compactifications. In a next post I-ll talk about the Horave-Witen model (an hterotic M-mtheory realization) whcis is particularly well siuted for phenomenologie and which has inspired well known areas of research such as the Randall-Sundrum models and the Ekppirotyc universe.
Wednesday, October 17, 2007
Nociones básicas sobre compactificación en teoria de cuerdas
Recordemos, las supercuerdas convencionales (las únicas de la que voy a hablar) se formulan en 10 dimensiones. Cómo el universo observado tiene la indecencia de no dar signo evidente de más de 4 hay que hacer algo para obtenerlo. Cómo bien explica el amigo Green lo que se hace es explotar la vieja teoría de Kalua-Klein de compactificar las dimensiones. Además uno saca la ventaja de que las isometrías del espacio compactificado se traducen en simetrías gauge. Las cuerdas tienen varias peculiaridades en las compactificaciones respecto a las teorías de campos puntuales, pero comparten una característica que es crucial. Resulta que cómo la compactificación se hace "a mano" no hay nada, en los casos más simples, que fije algunas características del espacio compactificado. En el caso más sencillo en que una sola dimensión se compactifica en un círculo la caracterísitica esencial es el radio. No hay nada uqe fije el tamaño del radio, es un parámetro libre. Y el problema es que algunas de las características del universo observado si dependen del valor exacto del radio. Si no lo podemos fijar teóricamente tenemos que las cuerdas ya tiene más parámetros libres y dejan de ser una teoría tan unificada (recuérdese que las cuerdas en principio sólo tiene un parámetro libre, la tensión de la cuerda).
La generalización más obvia de la compactificación en un n-toro, o sea, el producto de n-círculos. Aquí ya tenemos más estructura, y voy a analizar el caso del 2-toro para ejemplificar algunas cosillas útiles luego. No todos los toros son iguales, se distinguen unos de otros por la relación de tamaños de los radios. Esa relación nos describe familias de tornos no equivalentes bajo transformaciones conformes. Ese parámetro es lo que se conoce como móduli (luego daré una definición matemática más general, y como se calculan los móduli, el otro móduli del toro sería el tamaño de uno de los radios). Un aspecto que he mencionado, pero no he explicado, es que nada fija el valor del móduli. Pero ¿como debería fijarse ese valor? Bien, el moduli es un concepto geométrico, pero puede verificarse que en la toeria de cuerdas su valor siempre va a corresponder al valor esperado en el vacio (vev) de un campo escalar que aparece en la compactificación. El vev es básicamente el mínimo del potencial del campo. El problema es que los lagrangianos que describen la compactificacion no nos dejan ningún término de potencial para esos campos asociados a los móduli. Por eso permanecen indeterminados. Por poner un ejemplo sencillo, en el caso de compactificación en un círculo el campo asociado sería el (famoso en el mundillo) dilatón.
Bien, un círculo no vale como compactificación, que no nos da las dimensiones correctas, un 6-toro nos da las dimensiones correctas, pero deja demasiada simetría y no reproduce el modelo estándar ni de casualidad. Hay que ir a construcciones más complejas. Para poder entender bien algunas características esenciales luego explicaré ahora lo siguiente más sencillo que se puede hacer, compactificar en un orbifold. Un orbifold es lo que se conoce matemáticamente cómo conjunto cociente de un espacio topológico por al acción de un grupo finito. EL caso más simple puede verse como la acción de Z2 en el círculo. Esta puede verse que equivale a una identificación de las dos mitades de un círculo (respecto a un diámetro cualquiera), o sea, un segmento. El problema es que los dos extremos del diámetro son invariantes de la acción. Eso hace que el orbifold no sea un espacio suave, un manifold (o variedad, en español). Los puntos extremos son singularidades.
Llegados a este punto hay dos caminos, relativamente equivalentes. De un lado se puede comprobar que cierto tipo de estados, llamados twisted states, de la cuerda se propagan sin problemas en esas geometrías. Por otro lado se pueden eliminar esas singularidades mediante un proceso de "blowin-up" (o hinchado). El resultado del blowin up de un orbifold resulta ser un Calabi-Yau, de los que ahora hablaré. En ese blowin-up, la cuerda se propaga normalmente sin necesidad de estados twisteados (nada que ver con los twistors de Penrose pese al nombre) y tenemos dos descripciones matemáticas del mismo asunto.
Bien, vamos a los Calabi-Yaus. Las condiciones que se requieren alas cuerdas en 4 dimensiones es que tenga solo una carga supersimétrica (hay argumentos muy generales que indican que teorías con más de una supersimetría en 4 dimensiones no pueden ser consistentes). Aparte se pide que tengan algo llamado "holonomía SU(3)" y que sean Ricci flat, es decir, que su tensor de curvatura de Ricci sea nulo. Bien, el caos es que tenemos un espacio de 6 dimensiones reales con unas características precisas. Los matemáticos habían estudiado ya ese tipo de objetos, pero vistos como espacios complejos de dimensión (compleja) 3, y en particular de un tipo específico conocido como Khaler manifolds. Cómo curiosidad decir que la manera más sencilla d obtener calabi-Yaus es partir de espacios proyectivos complejos y hacer subespacios de los mismos definidos por polinomios homogéneos en variable compleja. La homogeneidad es requerida par ajustarse a que el espacio sea proyectivo. Reacuérdese que el plano proyectivo consiste en identificar todos los puntos de una recta, eso implica que sólo los polinomios homogéneos están bien definidos en el plano proyectivo.
Bien, el caso es que tenemos compactificaciones en Calabi-Yaus que nos dan aproximaciones muy buenas al modelo Standard si partimos de la cuerda heterótica. Esto esta bien, pero hay varias cosas que faltan. Un dato muy conocido de quien lea divulgación es que el número de generaciones de partículas se corresponde con un invariante topológico del Calabi-Yau, su característica de Euler. Hay otros aspectos de la física en 4 dimensiones que dependen de características topológicas, pero no todas, algunas, e importantes, dependen de la métrica del Calabi-Yau. Pues bien, en la época del libro, y de hecho hasta como quien dice antes de ayer, no se sabe calcular la métrica de un Calabi-Yau. Hoy día, quitando unos poquitos casos, las que se saben se obtienen, y con mucho trabajo, con métodos numéricos. ahí ya tenemos un avance.
Pero a ver, sigamos. Había dicho que necesitábamos saber el móduli space del Calabi-Yau. Para hacer eso lo que se hace es considerar la métrica del Calabi-Yau, no importa que no la sepamos, y variarla. Se impone que la nueva métrica siga siendo Ricci flat. Esto resulta en unas ecuaciones diferenciales.El número de soluciones de esas ecuaciones van a contar el número de modos independientes (en el sentido de dar las mismas topologías y supersimetrías) de modificar el Calabi-Yau. Los coeficientes de esas soluciones van a ser los modulis. En realidad los modulis no van por libre y definen ellos mismos un espacio geométrico. En ese espacio geométrico se puede dar una métrica. En algunos casos esos moduli spaces van a ser así mismo espacios de Khlaler. Normalmente se va a tener que le moduli consta de dos partes, una que nos da "la forma" (la relación de radios en el caso del toro) y otra que nos da el tamaño (el tamaño de uno cualquiera de los radios en el toro).
Espero que más o menos se me siga hasta aquí. Es que normalmente se pasa muy por encima en el tema este de la compactificación y es muy importante entenderlo medianamente bien para muchos aspectos importantes hoy día. Voy a ahora con algo que había omitido hasta ahora. Los Calabi-Yaus van a ser soluciones clásicas de la cuerda. Pero efectos perturbativos, y algunos no perturbativos, pueden cambiar eso. Uno de los efectos no perturbativos es la consideración de las D-branas. Resulta que la presencia de las D-branas esta relacionada con un aspecto que uno no esperaría en un Calabi-Yau. Algunos tipos de Calabi-Yaus, no compactos, tiene singularidades. En realidad es más preciso hablar de un conifold que de un Calabi-Yau en estos casos. Puede parecer que esto es muy técnico, y no se ajusta a nada "físico". Pero en realidad no es así. Estas peculiaridades son relevantes en dos aspectos. Uno el hecho de poder describir un
agujero negro mediante d-branaas enrolladas alrededor de cierto tipo de subvariedades del Calabi-Yau, conocidas cómo subvariedades de Lagrange (en realidad se puede calcular la entropía del black hole enrollando las branas en cosas más sencillas, como toros, pero el trabajo inicial usaba los Calabis). Otro aspecto, quizás más importante, es que esas singularidades del Calabi-yau, el conifold, permite que las cuerdas puedan realizar transiciones entre espacios con distintas topologias (obviamente en los puntos regularidades del Calabi-yau no se puede.
De todos modos con todas estas complejidades los Calabis, por si solos, no bastan. En un Calabi seguimos sin tener un potencial para el moduli. Hay que darle potencial a los modulis. La solución es peculiar. En los Calabis tenemos geometrías en que todos los campos de la cuerda, excepto la métrica, se anulan. Queremos considerar compactificaciones en que algunos campos de la cuerda, los supersimétricos que se pueden corresponder como campos gauge tomen valores no nulos. Esto es lo que se conoce como flux compactificacions, o compactificaciones de flujo. Se puede probar que en tales compactificaciones si se van a tener potenciales para los campos que determinan los valores de los moduli. Entonces ¿por que no se habían usado antes estas compactificaiones? de un lado porque se había demostrado que "eran imposibles". Pero se había demostrado antes de el descubrimiento de las d-branas. El truco esta en que algunos de estos campos gauge antisimétricos de los que hablo no pueden estar cargados respecto a al cuerda. Tiene que estar cargados respecto a D-Branas. Por tanto era imposible que se hubieran considerado estas compactificaciones antes del descubrimiento de las D-branas.
Otro aspecto muy interesante de estas compactificaciones de flujo es que son compatibles con compactificaciones "warped" (no sabría com traducirlo exactamente). En estas el espacio no va a ser ya un producto del espacio de Minkowky por el espacio interno, sino que estarán mezclados por un factor de warping, una exponencial decreciente de las coordenadas internas.
El hecho de que las compactificacioens de flujo permitan estas geometrías warped es lo que inspiro, como algo compatible con las cuerdas, los universos tipo Randal-Sundrum. En realidad ahí hay una dimensión de tamaño no planckiano (las compactificaciones tiene el orden del tamaño de Planck). Eso esta relacionado con que no se consideran solo compactificaicones de las teorías de cuerdas en 10 dimensiones. Se sabe que hay duales de las teorías de cuerdas que no son propiamente teorías de cuerdas, por ejemplo la teoria M. Otra de esas teorías es la teoría F (si la teoría M es dual de las supercuerdas tipo II A la teoría F es dual de la supercuerda tipo II B). Cierto tipo de compactificaciones de la teoría tipo II-B, que es dual a una compactificación de la teoria F, puede realizar, en la teoría de cuerdas, el modelo fenomenológico de Randall-Sundrum. Lo relevante es que la teoría M tiene 11 dimensiones, una más que la supercuerda. La teoría F, formulada como una libración elíptica de la cuerda tipo IIB, también (en otro formalismo tiene 12 dimensiones, pero una de esas dos dimensiones extra, respecto a la cuerda, es tipo tiempo, es decir, que hay dos dimensiones temporales). Lo peculiar es que esa dimensiones extra, respecto a las teorías de cuerdas, no tiene porque ser del tamaño de Planck de hecho no debería serlo.
Voy a cortar aquí, que si no nadie se va atrever con el post. Simplemente comentar que los modelos de Randall-Sundrum permiten cosas muy interesantes. Por ejemplo en ellos el gravitón se descompone en uno en 4 dimensiones, gravedad normal, y uno que puede moverse en la dimensión extra, el bulk, dando una modificación a la gravedad normal, y que hace que para distancias cortas la gravedad sea más fuerte. Eso posibilitaría (pero es improbable) que se formen agujeros negros en el CERN. Otra característica es que la energía de los modos masivos de la teoría de cuerdas, que normalmente serían del orden de la masa de Planck, tengan en realidad una masa que podría ser del orden de la energía del LCH (1 Tev). Esto abre la posibilidad de observar estados totalmente "cuerdistas" en el LHC (igualmente es muy improbable, y deberían distinguirse por sus productos de decay, no directamente). En fin, los warped universes son un submundo entero dentro de las cuerdas Aunque mucho de su estudio se puede hacer mediante modelos "fenomonologicos", o sea usando gravedad de Einstein + teorias de campos. Las cuerdas serían un motivante (y aparte permiten calcular algunos aspectos de los mismos, como el warp factor).
La generalización más obvia de la compactificación en un n-toro, o sea, el producto de n-círculos. Aquí ya tenemos más estructura, y voy a analizar el caso del 2-toro para ejemplificar algunas cosillas útiles luego. No todos los toros son iguales, se distinguen unos de otros por la relación de tamaños de los radios. Esa relación nos describe familias de tornos no equivalentes bajo transformaciones conformes. Ese parámetro es lo que se conoce como móduli (luego daré una definición matemática más general, y como se calculan los móduli, el otro móduli del toro sería el tamaño de uno de los radios). Un aspecto que he mencionado, pero no he explicado, es que nada fija el valor del móduli. Pero ¿como debería fijarse ese valor? Bien, el moduli es un concepto geométrico, pero puede verificarse que en la toeria de cuerdas su valor siempre va a corresponder al valor esperado en el vacio (vev) de un campo escalar que aparece en la compactificación. El vev es básicamente el mínimo del potencial del campo. El problema es que los lagrangianos que describen la compactificacion no nos dejan ningún término de potencial para esos campos asociados a los móduli. Por eso permanecen indeterminados. Por poner un ejemplo sencillo, en el caso de compactificación en un círculo el campo asociado sería el (famoso en el mundillo) dilatón.
Bien, un círculo no vale como compactificación, que no nos da las dimensiones correctas, un 6-toro nos da las dimensiones correctas, pero deja demasiada simetría y no reproduce el modelo estándar ni de casualidad. Hay que ir a construcciones más complejas. Para poder entender bien algunas características esenciales luego explicaré ahora lo siguiente más sencillo que se puede hacer, compactificar en un orbifold. Un orbifold es lo que se conoce matemáticamente cómo conjunto cociente de un espacio topológico por al acción de un grupo finito. EL caso más simple puede verse como la acción de Z2 en el círculo. Esta puede verse que equivale a una identificación de las dos mitades de un círculo (respecto a un diámetro cualquiera), o sea, un segmento. El problema es que los dos extremos del diámetro son invariantes de la acción. Eso hace que el orbifold no sea un espacio suave, un manifold (o variedad, en español). Los puntos extremos son singularidades.
Llegados a este punto hay dos caminos, relativamente equivalentes. De un lado se puede comprobar que cierto tipo de estados, llamados twisted states, de la cuerda se propagan sin problemas en esas geometrías. Por otro lado se pueden eliminar esas singularidades mediante un proceso de "blowin-up" (o hinchado). El resultado del blowin up de un orbifold resulta ser un Calabi-Yau, de los que ahora hablaré. En ese blowin-up, la cuerda se propaga normalmente sin necesidad de estados twisteados (nada que ver con los twistors de Penrose pese al nombre) y tenemos dos descripciones matemáticas del mismo asunto.
Bien, vamos a los Calabi-Yaus. Las condiciones que se requieren alas cuerdas en 4 dimensiones es que tenga solo una carga supersimétrica (hay argumentos muy generales que indican que teorías con más de una supersimetría en 4 dimensiones no pueden ser consistentes). Aparte se pide que tengan algo llamado "holonomía SU(3)" y que sean Ricci flat, es decir, que su tensor de curvatura de Ricci sea nulo. Bien, el caos es que tenemos un espacio de 6 dimensiones reales con unas características precisas. Los matemáticos habían estudiado ya ese tipo de objetos, pero vistos como espacios complejos de dimensión (compleja) 3, y en particular de un tipo específico conocido como Khaler manifolds. Cómo curiosidad decir que la manera más sencilla d obtener calabi-Yaus es partir de espacios proyectivos complejos y hacer subespacios de los mismos definidos por polinomios homogéneos en variable compleja. La homogeneidad es requerida par ajustarse a que el espacio sea proyectivo. Reacuérdese que el plano proyectivo consiste en identificar todos los puntos de una recta, eso implica que sólo los polinomios homogéneos están bien definidos en el plano proyectivo.
Bien, el caso es que tenemos compactificaciones en Calabi-Yaus que nos dan aproximaciones muy buenas al modelo Standard si partimos de la cuerda heterótica. Esto esta bien, pero hay varias cosas que faltan. Un dato muy conocido de quien lea divulgación es que el número de generaciones de partículas se corresponde con un invariante topológico del Calabi-Yau, su característica de Euler. Hay otros aspectos de la física en 4 dimensiones que dependen de características topológicas, pero no todas, algunas, e importantes, dependen de la métrica del Calabi-Yau. Pues bien, en la época del libro, y de hecho hasta como quien dice antes de ayer, no se sabe calcular la métrica de un Calabi-Yau. Hoy día, quitando unos poquitos casos, las que se saben se obtienen, y con mucho trabajo, con métodos numéricos. ahí ya tenemos un avance.
Pero a ver, sigamos. Había dicho que necesitábamos saber el móduli space del Calabi-Yau. Para hacer eso lo que se hace es considerar la métrica del Calabi-Yau, no importa que no la sepamos, y variarla. Se impone que la nueva métrica siga siendo Ricci flat. Esto resulta en unas ecuaciones diferenciales.El número de soluciones de esas ecuaciones van a contar el número de modos independientes (en el sentido de dar las mismas topologías y supersimetrías) de modificar el Calabi-Yau. Los coeficientes de esas soluciones van a ser los modulis. En realidad los modulis no van por libre y definen ellos mismos un espacio geométrico. En ese espacio geométrico se puede dar una métrica. En algunos casos esos moduli spaces van a ser así mismo espacios de Khlaler. Normalmente se va a tener que le moduli consta de dos partes, una que nos da "la forma" (la relación de radios en el caso del toro) y otra que nos da el tamaño (el tamaño de uno cualquiera de los radios en el toro).
Espero que más o menos se me siga hasta aquí. Es que normalmente se pasa muy por encima en el tema este de la compactificación y es muy importante entenderlo medianamente bien para muchos aspectos importantes hoy día. Voy a ahora con algo que había omitido hasta ahora. Los Calabi-Yaus van a ser soluciones clásicas de la cuerda. Pero efectos perturbativos, y algunos no perturbativos, pueden cambiar eso. Uno de los efectos no perturbativos es la consideración de las D-branas. Resulta que la presencia de las D-branas esta relacionada con un aspecto que uno no esperaría en un Calabi-Yau. Algunos tipos de Calabi-Yaus, no compactos, tiene singularidades. En realidad es más preciso hablar de un conifold que de un Calabi-Yau en estos casos. Puede parecer que esto es muy técnico, y no se ajusta a nada "físico". Pero en realidad no es así. Estas peculiaridades son relevantes en dos aspectos. Uno el hecho de poder describir un
agujero negro mediante d-branaas enrolladas alrededor de cierto tipo de subvariedades del Calabi-Yau, conocidas cómo subvariedades de Lagrange (en realidad se puede calcular la entropía del black hole enrollando las branas en cosas más sencillas, como toros, pero el trabajo inicial usaba los Calabis). Otro aspecto, quizás más importante, es que esas singularidades del Calabi-yau, el conifold, permite que las cuerdas puedan realizar transiciones entre espacios con distintas topologias (obviamente en los puntos regularidades del Calabi-yau no se puede.
De todos modos con todas estas complejidades los Calabis, por si solos, no bastan. En un Calabi seguimos sin tener un potencial para el moduli. Hay que darle potencial a los modulis. La solución es peculiar. En los Calabis tenemos geometrías en que todos los campos de la cuerda, excepto la métrica, se anulan. Queremos considerar compactificaciones en que algunos campos de la cuerda, los supersimétricos que se pueden corresponder como campos gauge tomen valores no nulos. Esto es lo que se conoce como flux compactificacions, o compactificaciones de flujo. Se puede probar que en tales compactificaciones si se van a tener potenciales para los campos que determinan los valores de los moduli. Entonces ¿por que no se habían usado antes estas compactificaiones? de un lado porque se había demostrado que "eran imposibles". Pero se había demostrado antes de el descubrimiento de las d-branas. El truco esta en que algunos de estos campos gauge antisimétricos de los que hablo no pueden estar cargados respecto a al cuerda. Tiene que estar cargados respecto a D-Branas. Por tanto era imposible que se hubieran considerado estas compactificaciones antes del descubrimiento de las D-branas.
Otro aspecto muy interesante de estas compactificaciones de flujo es que son compatibles con compactificaciones "warped" (no sabría com traducirlo exactamente). En estas el espacio no va a ser ya un producto del espacio de Minkowky por el espacio interno, sino que estarán mezclados por un factor de warping, una exponencial decreciente de las coordenadas internas.
El hecho de que las compactificacioens de flujo permitan estas geometrías warped es lo que inspiro, como algo compatible con las cuerdas, los universos tipo Randal-Sundrum. En realidad ahí hay una dimensión de tamaño no planckiano (las compactificaciones tiene el orden del tamaño de Planck). Eso esta relacionado con que no se consideran solo compactificaicones de las teorías de cuerdas en 10 dimensiones. Se sabe que hay duales de las teorías de cuerdas que no son propiamente teorías de cuerdas, por ejemplo la teoria M. Otra de esas teorías es la teoría F (si la teoría M es dual de las supercuerdas tipo II A la teoría F es dual de la supercuerda tipo II B). Cierto tipo de compactificaciones de la teoría tipo II-B, que es dual a una compactificación de la teoria F, puede realizar, en la teoría de cuerdas, el modelo fenomenológico de Randall-Sundrum. Lo relevante es que la teoría M tiene 11 dimensiones, una más que la supercuerda. La teoría F, formulada como una libración elíptica de la cuerda tipo IIB, también (en otro formalismo tiene 12 dimensiones, pero una de esas dos dimensiones extra, respecto a la cuerda, es tipo tiempo, es decir, que hay dos dimensiones temporales). Lo peculiar es que esa dimensiones extra, respecto a las teorías de cuerdas, no tiene porque ser del tamaño de Planck de hecho no debería serlo.
Voy a cortar aquí, que si no nadie se va atrever con el post. Simplemente comentar que los modelos de Randall-Sundrum permiten cosas muy interesantes. Por ejemplo en ellos el gravitón se descompone en uno en 4 dimensiones, gravedad normal, y uno que puede moverse en la dimensión extra, el bulk, dando una modificación a la gravedad normal, y que hace que para distancias cortas la gravedad sea más fuerte. Eso posibilitaría (pero es improbable) que se formen agujeros negros en el CERN. Otra característica es que la energía de los modos masivos de la teoría de cuerdas, que normalmente serían del orden de la masa de Planck, tengan en realidad una masa que podría ser del orden de la energía del LCH (1 Tev). Esto abre la posibilidad de observar estados totalmente "cuerdistas" en el LHC (igualmente es muy improbable, y deberían distinguirse por sus productos de decay, no directamente). En fin, los warped universes son un submundo entero dentro de las cuerdas Aunque mucho de su estudio se puede hacer mediante modelos "fenomonologicos", o sea usando gravedad de Einstein + teorias de campos. Las cuerdas serían un motivante (y aparte permiten calcular algunos aspectos de los mismos, como el warp factor).
Tuesday, October 16, 2007
Mental illness and scientific thought
Fist of all to advise the possible readers that despite the name of the entry this post will, at least partially, be kept on the topic of quantum gravity related arena to which this blog is devoted, concretelly to the problem of the colapse of the wave function and some purposed solutions, including "quantum conscence" theories. I certainly could write about many other non "quantum gravity" topics, in physic, science in general, or other areas of knowledge (nor to say "everyday life" topics) but I think that the eventual readers will feel better if they have a clear "editorial line" and knows what to expect.
But previously to speak about the central topic I´ll make a few disquisitions about the "crankpot" issue, partially because it is somewhat related to the sustainer of some atipic ideas, and partially because it is somewhat interesting in itself.
First let´s state some possible aceptions of the "cranckpot" term. The proper definiton of mental illnes would correspond to a professional of psicology. But as i´ll briefly discuss the acceptance of their definitions would imply that psicology would have a firm scientific status and curiously the term "cranckpot" is beeing used sometimes for people whose level of rigour is a few orders of magnitude upper to the one used ofthen in psicology, so "houston, houston, we have got a problem" ;-). For the shake of simplicity I´ll use some commonly accepted notions in psicology and some "common language" aceptions also, with the apropiate explanations when necessary. I´ll make a first broad distintion which will be, i hope, very helpfull. I´ll diferentiate "social related" mental illnes from "science" related ones.
In the field of "sociall related" mental insane scientifics we have some very famous ones. For example Kürt Göedel had some paranoic behaviours(in the commonly used sense of the term). He used to think that people wanted to put poisson in her foods, to international conspirations and similar things. Other, even more famous nowadays due to the book, and posterior film "a beateafull mind", is Jonh Nash. I have not readed the book and I am not sure if an aspect of the filmm is true or not, but I want to rescue it because I find it very interesting for the notion of a proper definition of "mentall illness". He, in the film, had alucinatory episodes where he saw (and heared) people who driven him to behave in a totally unaceptable social way. Concretelly the made him to belive that he was working for an inteligence goverment department. When the circunstances made him to realize that some particular persons that he saw were not "real" he clearly knew that he had a very serious problem. I guess that in reality He had a medical tratement with meds who made the alucintions to dissapear, but in the film (maybe in reality, it doesn´t matter for what I whant to wonder now) he relies in his logic to actually try to distinguish possilbe "alucinatory people" from real people (for example he says that one of the "ilusinary people", a girl, hadn´t grown for years which made clear for him that he couldn´t be real, even if his mind still madde him appear. Well, I find that this a very interesting question in itself. Science is, among other things, the aplication of logic to have fiable knowledge about the world. In this sense he was apliying it´s formation as a scientific to bypass a "bad work" of his perception. I have known personally people who have been prescribed mental disfunctions (maybe apropiatelly, maybe not) but who, despite it´s unusuall behaviour sometimes were very logical in it´s reasoning. Even if they considered very utipical, and scientific, ideas (an aspect unrelated to the problmatic social behaviour) such like considering the possible of telekinesis as real were able to accept that withouth a verificable under scientifics standards proofs of it that belief in t.k would be discarded. On the contrarie another person, whose social behaviour was never questioned as pathologic (nor I perosnally see why it could b otherwise), and who was a psicologyst itself, had the beief that some martial art prastice could allow some physically imposilbe things, like, for example, to defeat an opponent without actually touching it throught the use of "chi". Well , in this case the social and the scientific criteria (of respecting logic and it´s relation to proved, and verificable everywhere data) clearly gave a diferent answer to discern who was crazy and who not. If we go a litle bit far in this question we go into the problem of religions and in general "mistics" beliefs. In hiss book Time scape" the physicst and science ficition writer Gregory Benford rise the same question. From a purely scientific perspective the widelyy accepted religious beliefs are crazyness. He also stated that more "exotic" beliefs (evil possesions, communication with death people, etc) are commmon in a lot of people which otherwise were very conventinal in the social relations. What to think about ten?. I would even add that there is also a large amount of people who have a conventinal social behaviour, that don´t have any particular exotic belief but whose capabilitie to go into logical and scientific reasoning is null. People who are unable to do theminimally mental complex reasing and whose acceptance of "rational" ideas seems more due to the cassualities of their education that to any capability to discern by themselves sane from insane ideas. How to consider them.
I am going to add a las historic example, more for their interest in iself that for their importance in the rest of the post. I am talking about Newton in person. He joined in his person many of the previously asked questions. He had a very ugly social behaviour (sme modern spicologists analizing his biographys hipotesizes that he could have what is known as "Asperger symdrome"). He also had very deep religous beliefs (more of the 80% of his writes are reigious). Besides of his known scientific apportations he had worked in "alchemy", understood more in it´s magic implicatinos that in ther pre-chemical ones. Also in his pure scientific carrer he had made some risked experiments (he was near to end blind on one of his eyes becuase some atipical optical experiments. Well, said all this I think that I must add that it would not be just to totally judge his acts from a modern viewpoint. Before him sicence as we know it simply didn´t exist (It wouldn´t be exagerate to say thathe invented it). But that baby science didn´t explain a lot of things in the everyday life. I guess that it is not untill the achievement of the modern quantum mechanics (with the Schroedinger equation and inmediate developments) and it´s explanations of the chemics implied in everyday life that almost every earth commonly observed fact has (or hopfully has, despite it´s math complexity) an explanation under science. I think that it is more acceptable for a person in an almost totally unscientific world where almost every thing was far from a proper explanation to have magic, as well as religious beliefs. Althought on the other side Newton was a rationalist, or at leas that is relfected in another writng form Gregory Benford, wherewe see a modern physicist go to "ell" and finding there Newton who in all the years gone from it´s dead is tritying to made a "science" addecuate for hell, which can´t be an strictly rationalism science (becuase of the observable behaviour of hell).
Sic, I see that this historic remarks are very temptative and I have writen a lot withouth actually going into modern physics and it´s "crackpots". First I need a definiton of a "scientific crackpot". I mostly agree with the famouse one proposed By Jonh Baez. But I need to make a few comments. One of the examples proposed by Baez is Myron Evans. I had a knowledge of the Evans case prior to the knowledge of Baez. One friend of me has made his (brilliant, crowned with an article in nature) doctoral thesis in something called "topological electromagnetism". Basically it consists in a change of variables from the E and B fields to another ones which are apropiate to be used for an topolocial annalisis of the solutions. In particular if you do the usual compactification of R 3 by the point at infinite you get that his frontier S2. Well, you can see that the solutions of the Maxwell equations can be classifed by a topological quantitie related to the topological index (in the sense of the ides of Millnor)of the electric and magenetic fields viewed as funtions from S2 to S2. For a brief time I collaborated with my friend in a try to extend this ideas to Yang-Mills case, but it has passed a while from them and maybe I have explained bad some details (J.L, if you are reading this I invoke you to crrect possilbe mistakes ;-)). Well, the thing is that Myron Evans was interested in his works in order to publish a review of them in a forthcoming book publisehd by Elsevier devoted to Evans own ideas and related ones (like this of topological electromagnetism). We brieflly discused about the particular. But I think that it is out of place to say any more about this because of discreption (anyway, nothing offensive was said if someone worries about it). As a rsoult I tried to learn the work of Evans the problem was that none of the papers I coulr read for that time presented a complete description of them and referenced unavailable works. Well, that´is preciselly some of the cliams of Baez against Evans, I don´t know how actually the question is, but I wouldn´t want to centrate the question in Evans. He is only one well known exponent of uncommon scientific behaviour. Another name with an slighly similar problem is Podkeltnov. He claimed that a device, desgned for a diferent purpose that the one which mae it famous, with superconductors had "antigravitatory" behaviour. But he denied to give the precise configuration of the device because it could "give clouds" to other people who could thief his ideas. The last time I readed about it the NASA had repeated the experiment with a simplifeid desing without antigravitation (or to say properly,gravity shieldin). In this line also is the "Allais effect" of atipical behaviour of gravity while solar eclipses(Allais is a nobel prize in economy who has a formation as physicist). Similarly the last time I wondered about it the NASA was analizing a most precise version of his expermient. I think that the main reason these experiments are beeing considered by the NASA is because of the problem that the own NASA has with some of it´s satellites (I don´t just now remember the name, but it is a very famous open problem of unexplained gravitational anomalies).
Well, afther an enumeration of examples the definitin. A "scientific crackpot" would
be someone who defends an idea (that he belives very important) whose reliability is very unlikely and who, ofthem, refuse to give all the aspects of it because of being scared of "intelectual apropiation". I would distinguish here two cases. People without academic formation and people with it. I think it is not the same case somone whose maths doesn´t go, in the best of cases of basic calculus, from people who have a PhD in physicst, or maybe they are enigners. Those last people have (almost certainly) proved that at least in some part of his life had a proper knowledge of science. I guess that if they insist in presenting slopy ideas as fundamental advances, against the commmon belief, they are more suspectous of triying to gain more scientific recognition of what they deserve that really beliving "crazy" ideas. But this is not the end of the history. Not allways things are "black or white". There are some famouse cases where unlikely and marginated ideas in the end proved to be truth some years later (for example the theory of continental derive) so it is not just that easy to say for sure who is "scientifically" crazy or not. Even the lack of a math rigour is not always a criteria. The most famous case is Faraday, who is known but it´s famous law in electromagnetism. But it is less known that he had not mathformation and that he was guided mainly by intuition. Ok, nowadays a case just as Faraday is very unlikely, but apropiate translations of it coud happen i guess. And, of course, it would be unapropiate to relate "scientiic" to "social" crankpoptism.
Well, le´ts go, at last, with quantum mechanist. The most discused aspect of it is the problem of wavefuntion reduction. The most accepted viewpoint is the traditional, positivst, one "it works, don´t fix it". The "many words" Everet viewpoint is mathematically consistent but unboservable in practice. Decoherence seems the most realistic path (for a very good description of it I recomend to search into the web of another science fiction writer, Greg Egan, I am unable to find it just now the exact link). But there are more proposals. These days I have readed (mainly in railway travels as "ligh readin") a book by Illya prigogyne titled "the laws of chaos". Prigogyne, a very prestigious nobel prize in chemistry, has been worried for a long time by the problem of the "arrow of time" (not joke intended). In this short book he present a formulation of classical mechanist in a probablistic fashion. He forgetes about classical orbits and uses a probablity of finding a particle in a certain trayectory. He makes this for classical mechanis justifiying the change in the "dterministic chaos". The keypoint is that afther the "liapunov time" (the inverse of the Liapunov exponen for a chaotic system, which has the meaing of the time the system need to "forget" his initial condtion with an 90%, or somthing similar, I don´t remember exactly, of accuracy). Later he proposes a similar formulation of quantum mechanics. But quantum mechanics is allready probabilistic. Well, the trick is that hw worries about the norm of the wave funtion, and not the wavefuntion itself, which is what has a clear probabilistic interpretation. He studies an equation for it and he finds tht it has the same structurre that the equation for the classical case. So he has a equal formlation for classical and quantum echanist. I will nt dive into the detaills now. Simply to add that he need to use spectral theory for operators with complex spectrum, and that he uses "rigged Hilbert Spaces" instead of commmon Hilbert Spaces. In fact this last thing is not new, The proper formulation of Q.M. requieres it. A rigged Hilber space is an space with contains L2 funtions together with distributions (in ths Schwartz sense,, i.. linear operators in the hilber space, speaking looselly) whose action in the test functions (an apropiate subset of the Hilber space, usually integrable and infintely derivable functions)is finite. As I say it it can sound reasonable (or at least I hope so), but when you read the book you find a lot of wordy statements whose realiztion is not too clear. It is a divulgation intended book (althought it has a lot of maths and may be it would be more acurate to call it an "essay"). Well, it´s last statement is that his formalisms gives a precise meaining to the arrow time. I wouldn´t like to discuse to somone who belongs to the status "I have writen more papers in peer to peer reviews that more sicentfics have readed". But on the other sied Prigoyne is not a physician (chemistry, maby be mathematician because of his works in complexity theory) but I don´t have any percpetion about that his works would have gained mayor attention (even thought the book is form the 98). At least I can say for sure that it is not of mayor concern for string theorists.
A diferent resolution of the problem of the waveefuntion colapse is the "conscence" viewpoint. If I am not wrong the idea can be backdated to Bohm. The idea is that the observer, who in earth in the last case is allways an human beeing, is the responsible of the collapse because of an act of conscience (I recomend to read a S.F book of the above mentioned author, Greg Egan, about this respect "quarentena", it´is not my favourite S.F. Book, but it plays a lot with this idea). A more recent propnent of this idea is the vry famouse physics and mathematician Roger Penrose. The firs exposition of his ideas can be readed in his book "the empirors new mind". There he tires to convence to the reader that that colapse is related to quantum gravityon one side and to human brain on the other. He states that a computer (touring machine) can´t work like a human mind and that the sacpe to this is that Human mind is not a computer because he can reduce the wave funtion. Well, beeing such a prominent figure he has had foundings to teste hemirically his ides (it is a googd thing that it would be empirically estable). I know that the firs experiments were not as he expected, but I didn´t read the second book about this line of reseach "the shadows of mind". And althougth I have readed some chapters of his most recent book "the road to realliy" I haven preaded the chapters about thisparticualr concern. Let´s say that I find it very unlikel, but of course it is just a personal opinion and may perfectly be wrong. But Penrose is not the only proponent of this idea. Other not so famouse physicist have similar ideas, and not having behind them te sucesffull trayectorie of Penrose they not allways are so well accepted. I think that based only in this criteria it is inapropiate to state someone as crackpoopt (at least not if you are not ready to say that Penrose is, and I guess none whoud dare, among other things, becuas I guess nobody thinks that Penrose could be nearly something similar).
To end up this long post I´ll say a few more things about the problem of wavefuntion reduction. Some time ago a friend asked me to try to do a "as serious as possible" background for the film "the buterrfly effect". That fil trates time travels an time paradox. Well, I was persuaded and I did some considerations (not intended never as something serious). I did a premise, wht if we go an step further with he probablistic meaning of the wavefuntion?. I played with the interpretation that the wavefuntion in addendum with th probalbitity of finding a prticle in a particular possition it gave the probablity of finding it in a given time. This, of course, meaned that you neded to search a reason of why you coudn´t be sure of the time you are. I did many reaonings, but the more funny was this, let´s supoose that we have a time machine. We pose somone in it in a manner in which he can´t see the enviroment. In a given time he sees a dinnosaur inside the time machine (behind a glass wall that protects him, of course). Later the dinnosaurs exits the time machine and at last observer exits also from the time machine back to ehre, and "when" he had entered in it. The question is did he travel to the past or somone bring the dinno to the present? It is, of course, a time orinted analogy of the Einstein elevtor whcih drived him to the equivalence principle. This proposal can be elaborated deeper, and I do so form time to time. But at least up to day it is just a funny entertaining. In fact the idea has grown a lot more that it´s intial purpose, and seems an interesting approach to the "problem of time 2in canonical quantum gravity. But be sure that if I would have some candidat to great development in a precise mathe formulation I would have tried to publish it in a peer to peer review. But that is not the case, at least untill now, and for certain that I wouldnt try to publish ideas about this paritcular "cronoquantum mechanics" withouh haveing published a some more conventional articles ìn well known and firmly stablisehed topics. It is not the enviroment for risked ideas, even if presented as modest proposals, be sure of that my eventual readers ;-).
But previously to speak about the central topic I´ll make a few disquisitions about the "crankpot" issue, partially because it is somewhat related to the sustainer of some atipic ideas, and partially because it is somewhat interesting in itself.
First let´s state some possible aceptions of the "cranckpot" term. The proper definiton of mental illnes would correspond to a professional of psicology. But as i´ll briefly discuss the acceptance of their definitions would imply that psicology would have a firm scientific status and curiously the term "cranckpot" is beeing used sometimes for people whose level of rigour is a few orders of magnitude upper to the one used ofthen in psicology, so "houston, houston, we have got a problem" ;-). For the shake of simplicity I´ll use some commonly accepted notions in psicology and some "common language" aceptions also, with the apropiate explanations when necessary. I´ll make a first broad distintion which will be, i hope, very helpfull. I´ll diferentiate "social related" mental illnes from "science" related ones.
In the field of "sociall related" mental insane scientifics we have some very famous ones. For example Kürt Göedel had some paranoic behaviours(in the commonly used sense of the term). He used to think that people wanted to put poisson in her foods, to international conspirations and similar things. Other, even more famous nowadays due to the book, and posterior film "a beateafull mind", is Jonh Nash. I have not readed the book and I am not sure if an aspect of the filmm is true or not, but I want to rescue it because I find it very interesting for the notion of a proper definition of "mentall illness". He, in the film, had alucinatory episodes where he saw (and heared) people who driven him to behave in a totally unaceptable social way. Concretelly the made him to belive that he was working for an inteligence goverment department. When the circunstances made him to realize that some particular persons that he saw were not "real" he clearly knew that he had a very serious problem. I guess that in reality He had a medical tratement with meds who made the alucintions to dissapear, but in the film (maybe in reality, it doesn´t matter for what I whant to wonder now) he relies in his logic to actually try to distinguish possilbe "alucinatory people" from real people (for example he says that one of the "ilusinary people", a girl, hadn´t grown for years which made clear for him that he couldn´t be real, even if his mind still madde him appear. Well, I find that this a very interesting question in itself. Science is, among other things, the aplication of logic to have fiable knowledge about the world. In this sense he was apliying it´s formation as a scientific to bypass a "bad work" of his perception. I have known personally people who have been prescribed mental disfunctions (maybe apropiatelly, maybe not) but who, despite it´s unusuall behaviour sometimes were very logical in it´s reasoning. Even if they considered very utipical, and scientific, ideas (an aspect unrelated to the problmatic social behaviour) such like considering the possible of telekinesis as real were able to accept that withouth a verificable under scientifics standards proofs of it that belief in t.k would be discarded. On the contrarie another person, whose social behaviour was never questioned as pathologic (nor I perosnally see why it could b otherwise), and who was a psicologyst itself, had the beief that some martial art prastice could allow some physically imposilbe things, like, for example, to defeat an opponent without actually touching it throught the use of "chi". Well , in this case the social and the scientific criteria (of respecting logic and it´s relation to proved, and verificable everywhere data) clearly gave a diferent answer to discern who was crazy and who not. If we go a litle bit far in this question we go into the problem of religions and in general "mistics" beliefs. In hiss book Time scape" the physicst and science ficition writer Gregory Benford rise the same question. From a purely scientific perspective the widelyy accepted religious beliefs are crazyness. He also stated that more "exotic" beliefs (evil possesions, communication with death people, etc) are commmon in a lot of people which otherwise were very conventinal in the social relations. What to think about ten?. I would even add that there is also a large amount of people who have a conventinal social behaviour, that don´t have any particular exotic belief but whose capabilitie to go into logical and scientific reasoning is null. People who are unable to do theminimally mental complex reasing and whose acceptance of "rational" ideas seems more due to the cassualities of their education that to any capability to discern by themselves sane from insane ideas. How to consider them.
I am going to add a las historic example, more for their interest in iself that for their importance in the rest of the post. I am talking about Newton in person. He joined in his person many of the previously asked questions. He had a very ugly social behaviour (sme modern spicologists analizing his biographys hipotesizes that he could have what is known as "Asperger symdrome"). He also had very deep religous beliefs (more of the 80% of his writes are reigious). Besides of his known scientific apportations he had worked in "alchemy", understood more in it´s magic implicatinos that in ther pre-chemical ones. Also in his pure scientific carrer he had made some risked experiments (he was near to end blind on one of his eyes becuase some atipical optical experiments. Well, said all this I think that I must add that it would not be just to totally judge his acts from a modern viewpoint. Before him sicence as we know it simply didn´t exist (It wouldn´t be exagerate to say thathe invented it). But that baby science didn´t explain a lot of things in the everyday life. I guess that it is not untill the achievement of the modern quantum mechanics (with the Schroedinger equation and inmediate developments) and it´s explanations of the chemics implied in everyday life that almost every earth commonly observed fact has (or hopfully has, despite it´s math complexity) an explanation under science. I think that it is more acceptable for a person in an almost totally unscientific world where almost every thing was far from a proper explanation to have magic, as well as religious beliefs. Althought on the other side Newton was a rationalist, or at leas that is relfected in another writng form Gregory Benford, wherewe see a modern physicist go to "ell" and finding there Newton who in all the years gone from it´s dead is tritying to made a "science" addecuate for hell, which can´t be an strictly rationalism science (becuase of the observable behaviour of hell).
Sic, I see that this historic remarks are very temptative and I have writen a lot withouth actually going into modern physics and it´s "crackpots". First I need a definiton of a "scientific crackpot". I mostly agree with the famouse one proposed By Jonh Baez. But I need to make a few comments. One of the examples proposed by Baez is Myron Evans. I had a knowledge of the Evans case prior to the knowledge of Baez. One friend of me has made his (brilliant, crowned with an article in nature) doctoral thesis in something called "topological electromagnetism". Basically it consists in a change of variables from the E and B fields to another ones which are apropiate to be used for an topolocial annalisis of the solutions. In particular if you do the usual compactification of R 3 by the point at infinite you get that his frontier S2. Well, you can see that the solutions of the Maxwell equations can be classifed by a topological quantitie related to the topological index (in the sense of the ides of Millnor)of the electric and magenetic fields viewed as funtions from S2 to S2. For a brief time I collaborated with my friend in a try to extend this ideas to Yang-Mills case, but it has passed a while from them and maybe I have explained bad some details (J.L, if you are reading this I invoke you to crrect possilbe mistakes ;-)). Well, the thing is that Myron Evans was interested in his works in order to publish a review of them in a forthcoming book publisehd by Elsevier devoted to Evans own ideas and related ones (like this of topological electromagnetism). We brieflly discused about the particular. But I think that it is out of place to say any more about this because of discreption (anyway, nothing offensive was said if someone worries about it). As a rsoult I tried to learn the work of Evans the problem was that none of the papers I coulr read for that time presented a complete description of them and referenced unavailable works. Well, that´is preciselly some of the cliams of Baez against Evans, I don´t know how actually the question is, but I wouldn´t want to centrate the question in Evans. He is only one well known exponent of uncommon scientific behaviour. Another name with an slighly similar problem is Podkeltnov. He claimed that a device, desgned for a diferent purpose that the one which mae it famous, with superconductors had "antigravitatory" behaviour. But he denied to give the precise configuration of the device because it could "give clouds" to other people who could thief his ideas. The last time I readed about it the NASA had repeated the experiment with a simplifeid desing without antigravitation (or to say properly,gravity shieldin). In this line also is the "Allais effect" of atipical behaviour of gravity while solar eclipses(Allais is a nobel prize in economy who has a formation as physicist). Similarly the last time I wondered about it the NASA was analizing a most precise version of his expermient. I think that the main reason these experiments are beeing considered by the NASA is because of the problem that the own NASA has with some of it´s satellites (I don´t just now remember the name, but it is a very famous open problem of unexplained gravitational anomalies).
Well, afther an enumeration of examples the definitin. A "scientific crackpot" would
be someone who defends an idea (that he belives very important) whose reliability is very unlikely and who, ofthem, refuse to give all the aspects of it because of being scared of "intelectual apropiation". I would distinguish here two cases. People without academic formation and people with it. I think it is not the same case somone whose maths doesn´t go, in the best of cases of basic calculus, from people who have a PhD in physicst, or maybe they are enigners. Those last people have (almost certainly) proved that at least in some part of his life had a proper knowledge of science. I guess that if they insist in presenting slopy ideas as fundamental advances, against the commmon belief, they are more suspectous of triying to gain more scientific recognition of what they deserve that really beliving "crazy" ideas. But this is not the end of the history. Not allways things are "black or white". There are some famouse cases where unlikely and marginated ideas in the end proved to be truth some years later (for example the theory of continental derive) so it is not just that easy to say for sure who is "scientifically" crazy or not. Even the lack of a math rigour is not always a criteria. The most famous case is Faraday, who is known but it´s famous law in electromagnetism. But it is less known that he had not mathformation and that he was guided mainly by intuition. Ok, nowadays a case just as Faraday is very unlikely, but apropiate translations of it coud happen i guess. And, of course, it would be unapropiate to relate "scientiic" to "social" crankpoptism.
Well, le´ts go, at last, with quantum mechanist. The most discused aspect of it is the problem of wavefuntion reduction. The most accepted viewpoint is the traditional, positivst, one "it works, don´t fix it". The "many words" Everet viewpoint is mathematically consistent but unboservable in practice. Decoherence seems the most realistic path (for a very good description of it I recomend to search into the web of another science fiction writer, Greg Egan, I am unable to find it just now the exact link). But there are more proposals. These days I have readed (mainly in railway travels as "ligh readin") a book by Illya prigogyne titled "the laws of chaos". Prigogyne, a very prestigious nobel prize in chemistry, has been worried for a long time by the problem of the "arrow of time" (not joke intended). In this short book he present a formulation of classical mechanist in a probablistic fashion. He forgetes about classical orbits and uses a probablity of finding a particle in a certain trayectory. He makes this for classical mechanis justifiying the change in the "dterministic chaos". The keypoint is that afther the "liapunov time" (the inverse of the Liapunov exponen for a chaotic system, which has the meaing of the time the system need to "forget" his initial condtion with an 90%, or somthing similar, I don´t remember exactly, of accuracy). Later he proposes a similar formulation of quantum mechanics. But quantum mechanics is allready probabilistic. Well, the trick is that hw worries about the norm of the wave funtion, and not the wavefuntion itself, which is what has a clear probabilistic interpretation. He studies an equation for it and he finds tht it has the same structurre that the equation for the classical case. So he has a equal formlation for classical and quantum echanist. I will nt dive into the detaills now. Simply to add that he need to use spectral theory for operators with complex spectrum, and that he uses "rigged Hilbert Spaces" instead of commmon Hilbert Spaces. In fact this last thing is not new, The proper formulation of Q.M. requieres it. A rigged Hilber space is an space with contains L2 funtions together with distributions (in ths Schwartz sense,, i.. linear operators in the hilber space, speaking looselly) whose action in the test functions (an apropiate subset of the Hilber space, usually integrable and infintely derivable functions)is finite. As I say it it can sound reasonable (or at least I hope so), but when you read the book you find a lot of wordy statements whose realiztion is not too clear. It is a divulgation intended book (althought it has a lot of maths and may be it would be more acurate to call it an "essay"). Well, it´s last statement is that his formalisms gives a precise meaining to the arrow time. I wouldn´t like to discuse to somone who belongs to the status "I have writen more papers in peer to peer reviews that more sicentfics have readed". But on the other sied Prigoyne is not a physician (chemistry, maby be mathematician because of his works in complexity theory) but I don´t have any percpetion about that his works would have gained mayor attention (even thought the book is form the 98). At least I can say for sure that it is not of mayor concern for string theorists.
A diferent resolution of the problem of the waveefuntion colapse is the "conscence" viewpoint. If I am not wrong the idea can be backdated to Bohm. The idea is that the observer, who in earth in the last case is allways an human beeing, is the responsible of the collapse because of an act of conscience (I recomend to read a S.F book of the above mentioned author, Greg Egan, about this respect "quarentena", it´is not my favourite S.F. Book, but it plays a lot with this idea). A more recent propnent of this idea is the vry famouse physics and mathematician Roger Penrose. The firs exposition of his ideas can be readed in his book "the empirors new mind". There he tires to convence to the reader that that colapse is related to quantum gravityon one side and to human brain on the other. He states that a computer (touring machine) can´t work like a human mind and that the sacpe to this is that Human mind is not a computer because he can reduce the wave funtion. Well, beeing such a prominent figure he has had foundings to teste hemirically his ides (it is a googd thing that it would be empirically estable). I know that the firs experiments were not as he expected, but I didn´t read the second book about this line of reseach "the shadows of mind". And althougth I have readed some chapters of his most recent book "the road to realliy" I haven preaded the chapters about thisparticualr concern. Let´s say that I find it very unlikel, but of course it is just a personal opinion and may perfectly be wrong. But Penrose is not the only proponent of this idea. Other not so famouse physicist have similar ideas, and not having behind them te sucesffull trayectorie of Penrose they not allways are so well accepted. I think that based only in this criteria it is inapropiate to state someone as crackpoopt (at least not if you are not ready to say that Penrose is, and I guess none whoud dare, among other things, becuas I guess nobody thinks that Penrose could be nearly something similar).
To end up this long post I´ll say a few more things about the problem of wavefuntion reduction. Some time ago a friend asked me to try to do a "as serious as possible" background for the film "the buterrfly effect". That fil trates time travels an time paradox. Well, I was persuaded and I did some considerations (not intended never as something serious). I did a premise, wht if we go an step further with he probablistic meaning of the wavefuntion?. I played with the interpretation that the wavefuntion in addendum with th probalbitity of finding a prticle in a particular possition it gave the probablity of finding it in a given time. This, of course, meaned that you neded to search a reason of why you coudn´t be sure of the time you are. I did many reaonings, but the more funny was this, let´s supoose that we have a time machine. We pose somone in it in a manner in which he can´t see the enviroment. In a given time he sees a dinnosaur inside the time machine (behind a glass wall that protects him, of course). Later the dinnosaurs exits the time machine and at last observer exits also from the time machine back to ehre, and "when" he had entered in it. The question is did he travel to the past or somone bring the dinno to the present? It is, of course, a time orinted analogy of the Einstein elevtor whcih drived him to the equivalence principle. This proposal can be elaborated deeper, and I do so form time to time. But at least up to day it is just a funny entertaining. In fact the idea has grown a lot more that it´s intial purpose, and seems an interesting approach to the "problem of time 2in canonical quantum gravity. But be sure that if I would have some candidat to great development in a precise mathe formulation I would have tried to publish it in a peer to peer review. But that is not the case, at least untill now, and for certain that I wouldnt try to publish ideas about this paritcular "cronoquantum mechanics" withouh haveing published a some more conventional articles ìn well known and firmly stablisehed topics. It is not the enviroment for risked ideas, even if presented as modest proposals, be sure of that my eventual readers ;-).
Etiquetas:
foundations of quantum mechanics,
history of physics
Subscribe to:
Posts (Atom)