String dualities and M-Theory

I have changed the name of the blog to somewhat most "stringy" (that is, the possible dimensions of spacetiem in string theories). In fact it also was the usual califications I used to have in exams in a far past (and indded in the very last exam that I did, well, almost), that is, upper the maximum, but unfortunatelly I stopped to get that notes when they could have been more usefull. Anyway, the main reason is that I didnt´like the name of the journal and I neded something diferent, who knows if I´ll keep this name or I´ll change it. Let´s go now with the stuff.

One of the most important discoveries in string theory, the origin of the so called, second revolution, was to realize the fact (or at least to get firm evidence of) that the originally different string theories were in fact different aspects of a single theory. This somewhat remembers me one of the best known fable o Aesops (essopo in Spanish), the blind man and the elephant. There six blind man, presumably smart and knowledge people, had to describe how it was an elephant. One touched first the ear of the animal and said it was like an “bbanico” other touched first the nose (don’t know the English word for "trompa") and said it was like an snake, other touched the, er, "cola" (I really need to install an English Spanish dictionary) and thought that it was an string (obviously this was an string theorist :P) and so on.

Well, in string theory there is a slight analogy with the fable. Initially it was created the bosonic string, which needs 26 dimensions for it’s existence. From the very beginning it was obvious that it was mainly a toy theory. The universe that the physics study has fermions, so it was needed a theory which describes fermions. There were two ways to achieve this. One was introducing additional Grasman anticonmuting variables and writing an analogous of the Green-Schwartz lagrangian of the bosonic string. A different, and more useful for practical calculations, approach was to consider string theory s a theory of fields in the world-sheet (the two dimensional surface which is the evolution of a string). In addition to the bosonic fields X(s) which can be identified with the coordinates of the string, there were additional two dimensional fermionic fields which together formed an supersimetric multiplet. Until now there are some uniqueness, but it soon disappears.


In the bosonic string we have two types, open and closed strings (althought it is belived that a purelly interacting open string is inconsistent, loop diagrams of open strings should be equivalente to tree level closed string diagrams). A closed string comes from imposing periodic conditions to the fields, i.e. X(s + 2phi)=X(s). Well, for the superstring theory similar considerations must be held. Open superstring theoyr is known as Type I string theory. Closed string theory is known as type II.

But thing don´t end here. In adition to the periodic conditions for the bosonic fields you must add some periodicity conditions for the other fields. But for fermions it natural to have periodics as well as antiperiodic conditions. I will not dive into the detailss, but the final result is that you have two kinds of type II superstrings type A and type b.

But the thing doesn´t end there. In the worldsheet you have left moving and right moving fields. In the mid eighties Martinec et all created a new string theory by allowing that the left moving modes would be pure bosnic string theory wheil the left moving would be supersmultiplets. These are known as heterotic string theories. I speak of them in plural becuse there are two of them. You need to impose some conditions in the left moving bosonic fields so that they would result in anomaly free theories (basically that you compactify in an even dual self-latice). This has the consecuence that the heterotic theories are tied to simmety groups resulting from that compactification. The allowed groups are SO(32) and E(8)xE(8). Specially the second one is a very good candidate for unification of the standar model unification.

But with all this we have five consistent theories. That was somewhat ugly. In fact the expectation was the only good candidate to recover the standard model at low energies was the E(8)xE(8) heterotic string (b.t.w. soon afther the initial construction it was realized that you could get it by a diferent aproach, bosnization, which didn´t require that left moving "pure bosnic" modes, which were somewhat antiaestehic). But even so it was annoying to have self consisten theories which seemengly were useless.

The solution came from dualities. The word "duality" must be one of the more overused ones in math andn physic. Loosely speaking you can think that you have a dualitiy when you have diferent (and complementary) descriptions of the same phenomena.

Concretelly in string theory there are thre basic types of dualities. T, S and U duality.

T duality is a perturbative duality. I.e. is valid order by order in perturbation theory. To be honest I doubt that anyone whoe doesn´t know what a perturbaive solution is could be recomendto be reading this post, but anyway I´ll say a few things about it.

In quantum (or classic) mechanics only a few problems can be solved exactly -i.e. analitically-. Even linear problems can´t usually be solved exactlly. Fortunatelly in many practical cases you have that you can aproach the unsovlabel problem by a solvable one. That is you can get a separation of the form:

H=Hs + gHp

Here H is the full hamiltonian (or for what mattter lagrangian, i.e. a function(al) which describes the system. H s is the soluble part g is a constant, tipically small, and Hpis the perturbation hamiltonian. The tactic is to search for solutions of the form:

Φ= Φ₀ + gΦ₁ + g²Φ₂ + ....

That is, you have an infinite power series in the perturbative constant.

in quantum field theory, and for practical purposes, for string theory, Hs is always the ahmiltonina, or more usually lagrangina, for a free theoy, and Hp is tipically an interaction term. The perturbbative coupling is usually a couupling constant which describes the intensity of the interaction (for the coulmb law is the alpha constanct, which is related to the coulmb constant, for gravity it would be a constant related to the newton constant. The notation Φ comes fom the fact that in quantum mechanis the solution of a problem is a wave funtion, there is an perturbation theory fo rclassical mechanics, but i will not say anything about it.

Well, soon we will see why I have introduced these detailsl, but first I´ll explain what T duality is. The easiest ralization of T-duality is the compactification of one of the coordinates of the bosonic string in a circle of radius R. When you do that compactificaton you have that some closed strings can wrap the compactified dimension w times. That is known as the wraping number. Another aspect is thatin the compact dimensions the moment can´t be continous, it must be a discrete number, n.Well, you have that the thoeir compactified in a radius R is equal to a theorie compactified in a radius alpha/R if simultaneowulsy you exchange n and w.

For superstring theories you have similar T-dualities which relates some theories with anothers. But that´s not all the history. IN the mid ninties it was discover that in adition to strings (one dimensinoal objects) string theories needed to have upper dimensional objects whcih I´ll call, generally, p-branes where p indicates the dimensionality of the object. Tipically they will be Dp-branes.

Without going into the detaills, you can find some in this entry, you get that type II A theoir has even dimensinal Dp-Branes and that Type II b has odd dimensinal branes. If you do compactifications you have that in addition to relations betwen stirng related states, some Dp-branes of a theory are equivalent to anothers. As I discused in some previous post compactifications in a circle (or torus) are not realisitic. Some more realisitic compactifications are the Calabi-Yau spaces. There an analogous of T-Duality is cnjectured to exist under the name of mirror symmetry.

But even most important that T-duality is S-duality. This relates a weak coupling perturbative expansion for a theory for an strong coupling, non perturbative expansion of another theory. That is, if you exchange in a perturbative serie the coupling constant of a theory (typically represented by a field known as the dilaton field) by the inverse of the coupling of the other you have the same results. Aditionally you have there relations betwen the Dp-Branes. A particularlly spectacular case is that you can exhcange "fundamental" strings of one theory by D1-branes of the other (just for curiosity comment that the "magnetic" analogous of the tring is an NS5-brane. Well, the NS% brane of a theory is exchanged by a D5 brane of the other).


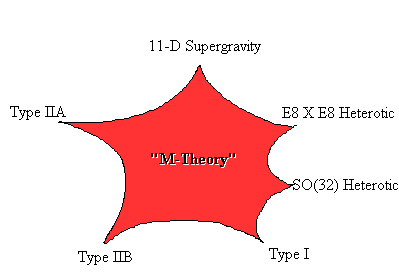
This images shows the web of dualities of string theory.

I have stated the resoults of the dualities, but haven´t said how one arrives to them. There various independent aproachs that give hints about this dualities. One of them is to get a low energy limt of stirng theoy, supergravity theories in the apropiate dimension. A particularllyniteresting thing comes form this.

In type II A theory you have a colection of Do-branes which look like somthing simlilar to what is known as a "kaluza klein tower". This KKT usually is a signal of an aditional dimension. That is, you have an indications of an eleventh dimension. The size of that diemsnion is related to the coupling constant,λ, of the type II A theory by the relation:

R=λ^2/3.

There are aditional suport for this relation. For example 11 dimensinal supergravity compactified apropiately is equivalent to the 10 dimensional supergravity which is the low energy limit of type II A string theory.

This 11 dimensional theoy is known as M-Theoy. There is not a precise formulation of it (and it is suspected that it has not a classical limit which allows to give a lagrangian for it). Despite this there are ways to relate it to the other string theories. So the general picture emerging from all this is that there is a single theorie, whcih perturbative form can be described by a theory of fundamental strings. And the diferent limits of it are the known strings.

But not all of the limits are necessrally good candidates to represent the observed universe. Nowadays the most promising candidates are a particular limit of M-Theory which aproachs it to the heterotic strings, known as "heterotic M-theory" and a particular kind of compatifications of Type II theories kown as "lux compactifications. In a next post I-ll talk about the Horave-Witen model (an hterotic M-mtheory realization) whcis is particularly well siuted for phenomenologie and which has inspired well known areas of research such as the Randall-Sundrum models and the Ekppirotyc universe.